Resultats de la cerca
Es mostren 61 resultats
corbes bitangents
Matemàtiques
Dues corbes que tenen dos punts en els quals són mútuament tangents.
corbes de Lissajous
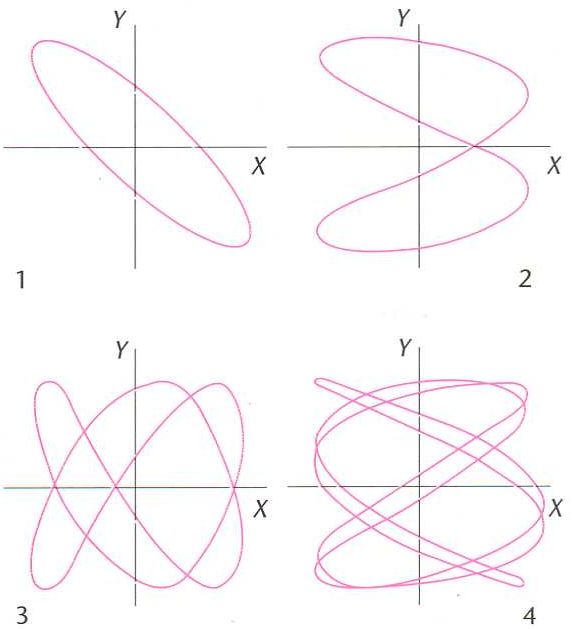
Corbes de Lissajous la relació entre les pulsacions wx i wy dels dos moviments corresponents.
© Fototeca.cat
Matemàtiques
Corbes que apareixen en la composició de dos moviments vibratoris harmònics perpendiculars entre ells.
Hom obté corbes molt diverses, en general obertes, però, si la relació entre els períodes dels dos moviments és racional, la corba obtinguda és tancada i el moviment resultant és periòdic si els dos períodes són iguals, la corba resultant és una circumferència o una ellipse Hom les pot reproduir fàcilment en un oscilloscopi fent que les tensions horitzontal i vertical siguin sinusoidals
corba
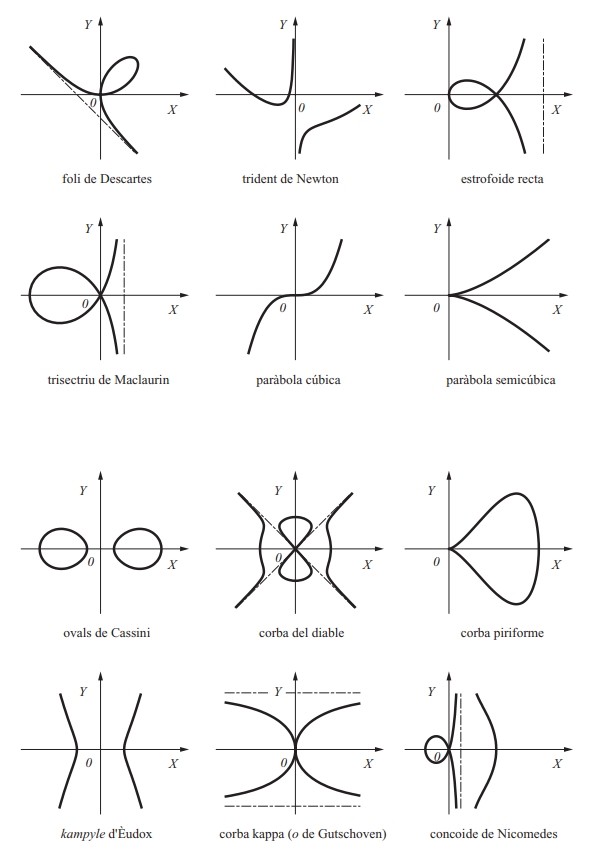
Corbes cúbiques i quàrtiques
Matemàtiques
Lloc geomètric que és la trajectòria d’un punt que es mou amb un sol grau de llibertat.
Una corba sempre pot ser considerada com una infinitat simple de punts, i aquest és el plantejament adoptat pels matemàtics en l’estudi de les corbes contínues topologia En aquest sentit, una corba és el conjunt de punts de ℝ n que és homeomorf amb un interval a , b ⊂ ℝ Seguint Menger hom podria considerar les corbes al pla espai com a objectes de dimensió topològica 1 ja que tota circumferència superfície esfèrica de centre un punt de la corba la talla en un conjunt de punts de dimensió zero punts que són centres de circumferències superfícies…
evolvent
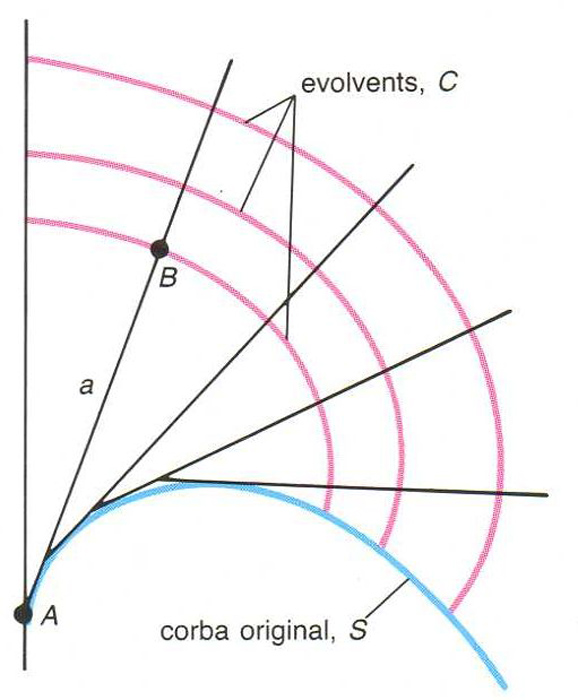
Les corbes C són les evovlents de S
© fototeca.cat
Matemàtiques
Donada una corba S
, cadascuna de les corbes ortogonals a les tangents de S
.
Si C és una envolvent de S , S és l'evoluta C Donada la corba S , hom pot generar una evolvent tot fixant una tangent a S en un punt de tangència A , limitant-ne la seva longitud a i anant-la enrotllant a la corba, de manera que el punt extrem B determina una evolvent Les diferents longituds a determinen les diferents evolvents
corba d'ompliment
Matemàtiques
Corba contínua que passa per tots els punts d’una regió fins a omplirla enterament.
Les corbes d'ompliment més conegudes són les corbes de Peano
unicursal
Matemàtiques
Dit de la corba algèbrica plana de gènere zero.
Puix que el gènere p és donat per la fórmula p = n -1 n -2/2-δ- k , on n és el grau de la corba, δ el nombre de punts nodals, k el nombre de punts cuspidals, són corbes unicursals les còniques n =2, les cúbiques amb un punt doble o cuspidal n =3, δ=1, k =0 o bé n =3, δ=0, k =1, les quàrtiques amb tres nodes n =4, δ=3, etc La característica intuïtiva de les corbes unicursals és que poden ésser recorregudes d’una sola tirada passant, si cal, per l’infinit El gènere i, per tant, el caràcter de corba unicursal p =0 és invariant per a les transformacions algèbriques
superfície reglada
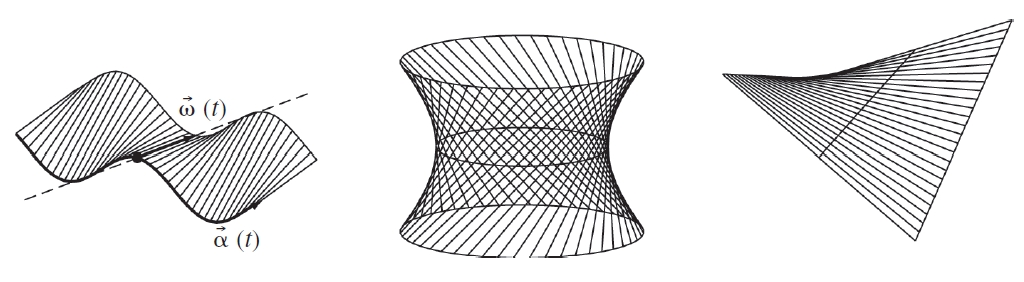
Superfícies reglades
Matemàtiques
Superfície engendrada per una família infinita de rectes que depenen d’un paràmetre.
Cadascuna d’aquestes rectes és anomenada generatriu de la superfície els procediments habituals per a definir-les són donar les equacions d’una recta en l’espai amb un paràmetre variable, o bé donar tres corbes directrius i prendre com a generatrius les rectes que recolzen sobre aquestes tres corbes Hi ha dues classes de superfícies reglades si en tots els punts d’una mateixa generatriu la superfície té el mateix pla tangent, es tracta d’una superfície desenvolupable , i la superfície pot ésser construïda cargolant oportunament un o diversos trossos de paper però si…
ruleta
Matemàtiques
Trajectòria descrita per un punt d’una corba, anomenada rodolant, que rodola sobre una altra anomenada base (rodolament).
Els exemples més coneguts són els de les corbes anomenades cicloide, epicicloide i hipocicloide
singular
Matemàtiques
Dit del punt d’una corba o d’una superfície que no és ordinari (o simple), és a dir, que és isolat, o no admet tangent, o és un punt d’encreuament.
És un concepte clau de la geometria diferencial en l’estudi de corbes i superfícies
Maryam Mirzakhani

Maryam Mirzakhani
© Stanford University
Matemàtiques
Matemàtica iraniana.
El 1994 i el 1995 guanyà les medalles d’Or de les Olimpíades Internacionals de Matemàtiques per a estudiants no universitaris El 1999 es graduà a la Universitat Tecnològica de Sharif Teheran i posteriorment ingressà a la Universitat de Harvard, on preparà la tesi doctoral amb Curtius McCullen 2004 En 2004-08 treballà al Clay Mathematics Institute i fou professora a la Universitat de Princeton Aquest darrer any s’incorporà com a docent a la Universitat de Stanford El seu camp d’estudi se centrà en la topologia de dimensió baixa, i una de les seves primeres aportacions destacades fou la…
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- Pàgina següent
- Última pàgina