Resultats de la cerca
Es mostren 11 resultats
enter
Matemàtiques
Classe d’equivalència que la relació (a,b)R(c,d), si, i només si, a+d = b+c, indueix en el conjunt producte ℕ × ℕ (ℕ essent el conjunt dels nombres naturals).
El conjunt d’aquestes classes d’equivalència conjunt quocient és el conjunt dels nombres enters ℤ = {0, ±1, ±2, ±3, } Hom anomena representant canònic d’un enter a,b aquell en què o a o b és 0 Si l’esmentat representant canònic és de la forma m, 0, aquest és un enter positiu , representat també per + m si és la forma 0, m , es tracta d’un enter negatiu , habitualment representat per - m i si és 0,0, és l' enter nul , o sigui 0 En el conjunt ℤ hom defineix dues operacions la suma és definida per a, b + c, d = a + c , b + d , i el producte , per a, b c, d = ac + bd, ad + bc Tal…
Elements
Matemàtiques
Tractat de matemàtiques atribuït a Euclides i que ha estat, fins a mitjan segle XIX, l’autoritat màxima dins el camp de les matemàtiques generals.
Sintetitzà perfectament el treball dels antics matemàtics grecs i li donà una major coherència lògica amb les noves definicions de línia i de pla i, sobretot, amb la introducció del cinquè postulat millorà també l’ordenació i les demostracions de les proposicions Malgrat ésser un text de compilació, hom no pot posar en dubte que la planificació global de l’obra i el mètode expositiu, com també un bon nombre dels seus teoremes, són obra del mateix Euclides
funció de risc
Matemàtiques
Funció que constitueix un dels elements essencials en la teoria de la decisió estadística i que representa l’esperança matemàtica de la pèrdua L.
Donat un espai de probabilitat H , A , M i una variable aleatòria x a valors en ℝ k i dependent d’un h ∈ H amb funció de densitat f h , hom considera les funcions de decisió d que a cada vector x 1 , , x n de valors de n variables independents amb la mateixa llei de x , associen una decisió Així mateix, la funció de pèrdua L h, d mesura la pèrdua produïda quan l’estat h és dut a terme i la decisió és presa La funció de risc és definida aleshores mitjançant la fórmula Hi ha altres possibles definicions, una mica més complicades Cal fer notar que en la funció de risc la…
mitjana
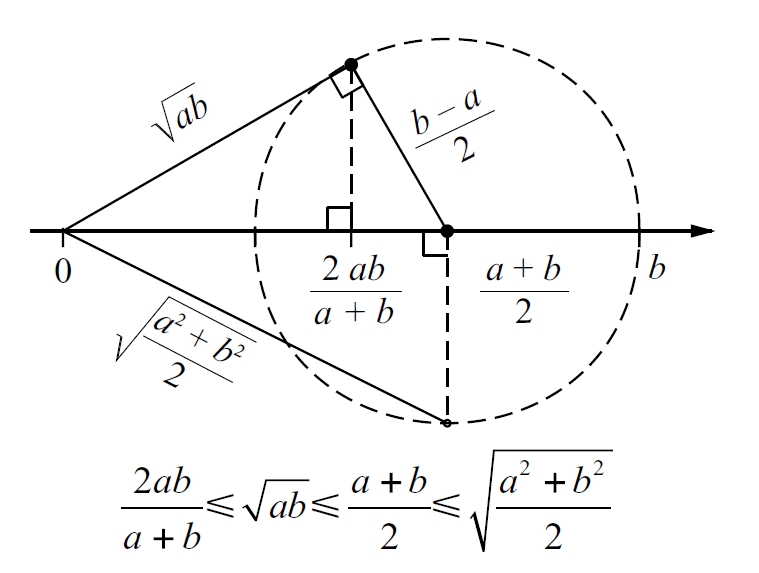
Mitjanes dels nombres a i b: harmònica, geomètrica, aritmètica i quadràtica
© fototeca.cat
Matemàtiques
Donats n valors o observacions x1, x2, ..., xn, valor x definit com la suma de tots ells dividida per llur nombre, és a dir, .
La mitjana x així definida és anomenada també mitjana aritmètica i valor mitjà Si les observacions constitueixen el conjunt de la població, x serà la mitjana de la població , mentre que si les observacions són d’una mostra aleatòria de la població mostreig, x és la mitjana de la mostra A la pràctica, la mitjana de la població és normalment desconeguda, i hom utilitza com a estimació la mitjana d’una mostra Quan les observacions poden ésser agrupades en k classes, amb efectius respectius n 1 , n 2 , , n k i freqüències respectives f 1 , f 2 , , f k , la fórmula per al càlcul de la mitjana és…
teoria de la computació
Matemàtiques
Branca de les matemàtiques que estudia problemes de decidibilitat.
Com és usual en la història de les matemàtiques, té orígens aparentment molt diferents que finalment conflueixen i permeten d’establir el que esdevé una teoria enormement potent i irrenunciable Cal remarcar-ne el problema diofàntic plantejat per David Hilbert l’any 1900, i el problema de les paraules que sorgí en el món de la topologia algèbrica Es tracta de dos problemes típics de decidibilitat és a dir, aquells en què cal disposar d’un mètode que permeti de decidir una o altra de dues opcions atesa una equació diofàntica, té solució, són equivalents dues paraules donades per endavant L’any…
trigonometria

1, circumferència de referència per a la definició de les raons trigonomètriques; 2, representació gràfica de les línies trigonomètriques; 3, símbols emprats en la resuloció de triangles
© fototeca.cat
Matemàtiques
Part de la matemàtica inicialment dedicada a l’estudi de les relacions entre les amplituds dels angles i les longituds dels segments que llurs costats determinen en les rectes que tallen.
La trigonometria es basa en les propietats de les anomenades raons trigonomètriques , que són definides a partir d’un punt P x,y d’una circumferència de centre O i per l’angle α que forma el radi r = OP amb l’eix OX , mitjançant els sis quocients següents sin α = y/r sinus cos α = x/r cosinus tg α = y/x tangent cotg α x/y cotangent sec α = r/x secant cosec α = r/y cosecant Quan el punt P és a una distància r = 1 de l’origen O , el valor absolut d’aquestes raons és representat per la longitud de certs segments anomenats línies trigonomètriques , respectivament, fàcils de traçar A partir de…
anàlisi matemàtica

anàlisi matemàtica Portada dels Philosophiae Naturalis Principia Mathematica de Newton (1687)
© Fototeca.cat
Matemàtiques
Part de les matemàtiques bastida sobre els conceptes bàsics de funció, límit, continuïtat, derivada i integral.
És el desenvolupament modern del càlcul infinitesimal, elaborat durant els segles XVII i XVIII, que tenia com a principals problemes el de les quadratures determinació de la longitud d’una corba i de les àrees i volums de figures i el de la tangència traçat de tangents a corbes i superfícies Els coneixements que s’anaren acumulant sobre aquests temes formaren els càlculs integral i diferencial, cor d’aquesta disciplina matemàtica L’anàlisi matemàtica presenta els trets distintius de l’abstracció i generalitat dels seus mètodes, característics del rigor del raonament lògic És el resultat d’una…
mesura
Matemàtiques
Aplicació m definida entre una àlgebra de conjunts ɑ d’un espai mesurable (Ω, ɑ) i el conjunt ℝ+ dels nombres reals positius.
L’aplicació compleix que la mesura de la unió de dos conjunts A i B de ɑ és igual a la suma de les respectives mesures, és a dir ∀ A ∈ ɑ i ∀ B ∈ ɑ tals que A ∩ B = ∅, m A + m B La terna Ω, ɑ, m és anomenada espai de mesura , i els conjunts de l’àlgebra ɑ són anomenats mesurables En el cas que ɑ sigui una σ-àlgebra de Borel, una mesura m és anomenada σ-additiva si la mesura d’una unió infinita i numerable de conjunts de ɑ disjunts dos a dos és igual a la suma de les respectives mesures, és a dir essent A i ∈ ɑ i A i ∩ A j = ∅, per a tot i, j tals que i ≠ j Una mesura és anomenada fitada…
geometria
Matemàtiques
Part de la matemàtica basada en la intuïció d’espai.
El nom prové de la seva primera aplicació la mesura de la Terra Els diversos apartats en què hom divideix la geometria fan referència a la natura dels objectes d’estudi i al mètode emprat Per a una definició unitària de la geometria elemental, l’any 1872 CF Klein proposà,en el “programa d’Erlangen”,la noció de geometria com a consideració d’un espai el conjunt dels punts i un grup de transformacions d’aquest espai, els invariants del qual serien les nocions de la geometria en qüestió El primer estudi de la geometria fou de caràcter intuïtiu, i consistí en la compilació de fets relatius a…
conjunt

Representació gràfica de la relació de pertinença i de les operacions d’unió i intersecció dels conjunts
© Fototeca.cat
Matemàtiques
Reunió d’objectes ben definits en la intuïció o en el pensament, considerada com una totalitat (Cantor).
Aquesta definició, des del punt de vista matemàtic, no és vàlida, i, així, en matemàtiques la noció de conjunt no és definida, i s’inclou dins del desenvolupament d’una teoria axiomàtica que eviti les paradoxes i contradiccions com les que, a començament del segle XX, posaren en qüestió no solament la teoria de conjunts, sinó bona part de la matemàtica Hom no defineix, doncs, ni conjunt, ni element, ni la relació de pertinença, i es conforma amb la idea intuïtiva del que signifiquen frases com Un conjunt és format per elements, o l’element 4 pertany al conjunt dels nombres naturals La…