Resultats de la cerca
Es mostren 9 resultats
polhòdia
Física
Matemàtiques
Corba que descriu sobre l’el·lipsoide el punt de contacte d’un el·lipsoide d’inèrcia amb el pla en què aquest roda.
Geomètricament, és definida pels punts de l’ellipsoide en què el pla tangent equidista del centre de l’ellipsoide El pol terrestre descriu una polhòdia sobre la superfície del planeta, a causa del moviment de precessió de l’eix de rotació de la Terra al voltant de l’eix d’inèrcia
Abū ‘Alī al-Ḥasan ibn al-Hayṯam
Astronomia
Física
Matemàtiques
Astrònom, matemàtic i físic àrab conegut a Occident amb el nom d’Alhazen.
Es traslladà a Egipte, on proposà al califa fatimita al-Hākim un sistema per a regular les crescudes del Nil La seva obra més coneguda és el tractat d’òptica Kitāb al-manaẓir , on descriu l’ull amb una gran exactitud
autòmat finit determinista
autòmat finit determinista
Matemàtiques
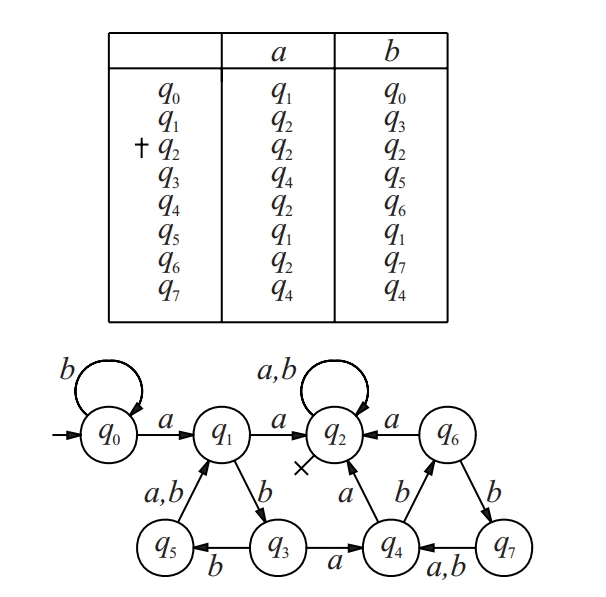
Estructura de la forma M = (Q, ∑, δ, q0, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet, anomenat d’entrada; δ : Q ⨉ ∑* → Q és la funció de transició que satisfà ∀q ∈ Q, ∀x,y ∈ ∑*:δ(q, λ) = q, δ(q, xy) = δ(δ(q, x), y) essent xy la concatenació de x i de y, i λ la paraula buida i ∑* el conjunt de paraules; q0 ∈Q s’anomena estat inicial; F ⊂ Q s’anomena conjunt d’estats finals o acceptadors.
Usualment un autòmat finit determinista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si δ q i , a = q j S’indica l’estat inicial amb una fletxa i els finals amb una creu
autòmat finit indeterminista
autòmat finit indeterminista
Matemàtiques
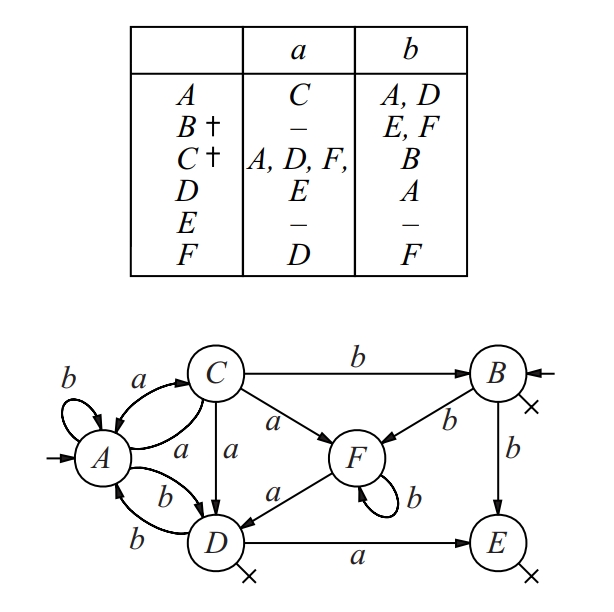
Estructura de la forma M = (Q, ∑, δ, I, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet anomenat d’entrada; δ : 2Q ⨉ ∑* → 2Q és la funció de transició que satisfà ∀P1, P2 ⊂ Q, ∀x, y∈∑*: δ(∅, x) = ∅, δ(P1, λ) = P1, δ(P1 ∪ P2, x) = δ(P1, x) ∪ δ(P2, x), δ(P1, xy) = δ(δ(P1, x)y), essent xy la concatenació de x i de y i ∑* el conjunt de paraules; I ⊂ Q és el conjunt d’estats inicial; F ⊂ Q és el conjunt d’estats finals o acceptadors.
Usualment un autòmat finit indeterminista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si q j ∈ δ q i , a S’indiquen els esstats inicials amb fletxes i els finals amb una creu Els llenguatges acceptats pels autòmats finits indeterministes són els mateixos que els reconeguts pels finits deterministes regulars L’avantatge dels indeterministes enfront dels deterministes és la facilitat de maneig i de construcció
trocoide
Trociode
© fototeca.cat
Matemàtiques
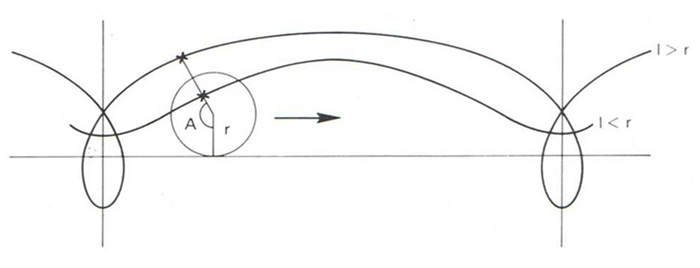
Corba descrita per un punt fixat a un cercle quan aquest cercle roda sense lliscament sobre una línia recta fixa.
Si el radi del cercle és r , la distància del punt generador al centre del cercle és l i A és l’angle determinat pel punt quan el cercle ha rodat A radiants, aleshores les equacions paramètriques de la trocoide són x = rA-l sin A y = r-l cos A Si l és major que r punt exterior al cercle, la trocoide descriu rulls si l és menor que r punt interior al cercle, la trocoide no toca mai la línia recta fixa base del desplaçament si el punt és el centre del cercle, la trocoide és una recta si l és igual a r punt de la circumferència, la trocoide és aleshores una cicloide
herpolhòdia
Física
Matemàtiques
Corba que el punt de contacte d’un el·lipsoide d’inèrcia descriu en el pla sobre el qual rodola (polhòdia).
Josep de Saragossa i Vilanova
Astronomia
Matemàtiques
Matemàtic i astrònom.
Mestre en arts a la Universitat de València, interessat des de jove per les matemàtiques, no acceptà una càtedra a la universitat per professar a la Companyia de Jesús Residí en diverses ciutats, fou professor al collegi de l’orde a Mallorca, on estigué en contacte amb l’historiador i matemàtic Vicent Mut Ensenyà després a Barcelona, i el 1660 passà al collegi de Sant Pau de València, on es dedicà a l’estudi i l’ensenyament de matemàtiques i a l’observació astronòmica El 1670 fou nomenat titular de la càtedra de matemàtiques del collegi de Sant Isidre de Madrid, on restà els darrers anys de…
anàlisi factorial
Psicologia
Matemàtiques
Tècnica estadística que descriu i explica les relacions entre unes variables aleatòries, directament observables, i unes altres de latents, també aleatòries, anomenades factors, que poden ser causa de les primeres.
D’ús freqüent en la investigació experimental psicològica i pedagògica, és basada en la teoria de les correlacions i té per objecte de manifestar el grau de variabilitat comuna existent en un cert camp de fenòmens cada una de les dimensions d’aquesta variabilitat és anomenada factor, i n'existeixen de diversos ordres entre ells cal diferenciar els comuns i els específics S'aplica, sobretot, en l’estudi de les diferències individuals i en la indagació de les aptituds i les qualitats de la personalitat L’iniciador fou Charles Spearman, el 1904, amb la teoria bifactorial, i un dels més grans…
helicoide
Matemàtiques
Superfície generada per una semirecta R, l’extrem de la qual recorre una línia recta D, a la qual es manté sempre perpendicular, de manera que qualsevol punt fix M de la semirecta descriu una hèlix que té R per eix.
La semirecta R és la generatriu de l’helicoide