Resultats de la cerca
Es mostren 66 resultats
desenvolupament
Matemàtiques
Operació consistent a desplegar sobre un mateix pla els elements successius d’una superfície desenvolupable
.
desenvolupament en sèrie
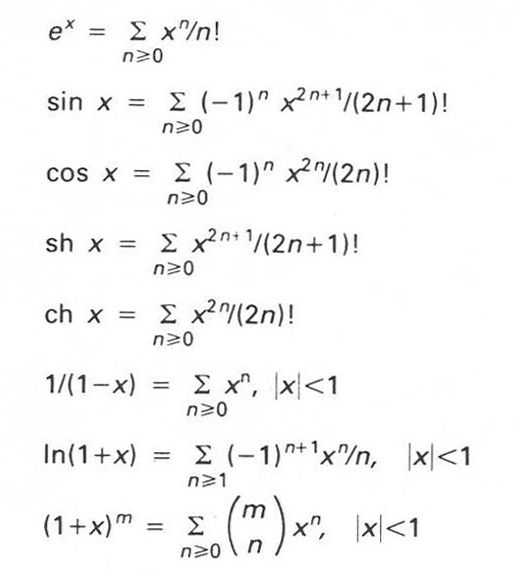
Desenvolupament en sèrie de potències d’algunes funcions
©
Matemàtiques
Expressió d’una funció real, de variable real o complexa,
f(x) ∞
, en termes d’una sèrie de funcions
:
.
La legitimitat d’aquesta igualtat depèn de la convergència de la successió de sumes parcials, en el domini de definició de fx Hom empra, generalment, el desenvolupament en sèrie de potències o sèrie entera, que resulta del teorema de Taylor , i, en el cas de funcions periòdiques, hom empra el desenvolupament en sèrie de Fourier anàlisi de Fourier
superfície desenvolupable
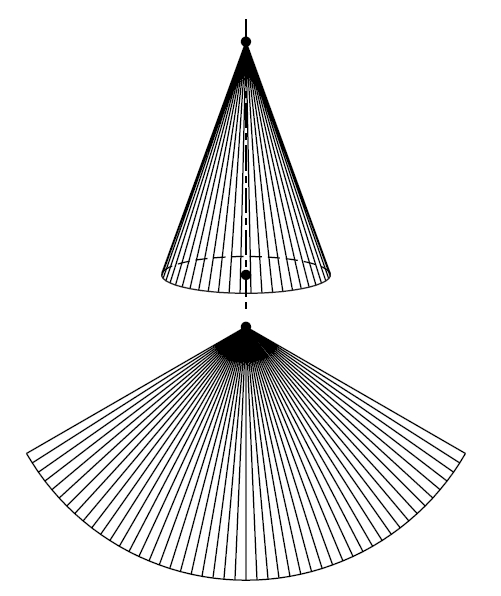
Superfície desenvolupable i el seu desenvolupament
Matemàtiques
Superfície isomètrica al pla, és a dir, que hom pot desplegar sense deformació sobre un pla.
Perquè una superfície sigui desenvolupable cal que contingui rectes superfície reglada i que el vector normal a la superfície sigui constant al llarg de cada recta En són exemples els cons, els cilindres i les superfícies constituïdes per totes les tangents a una corba en l’espai Qualsevol superfície desenvolupable és d’un d’aquests tres tipus citats
polinomis de Bernoulli
Matemàtiques
Polinomis Φn(x) definits pel desenvolupament
En termes dels nombres de Bernoulli s’expressen com Hom empra els polinomis de Bernoulli en fòrmules d' integració numèrica i en càlcul de diferències finites
Abū-l-Wafā’ al-Buzǧānī
Matemàtiques
Matemàtic àrab que contribuí al desenvolupament de la trigonometria.
És autor del Kitāb al-handasa ‘Tractat de geometria’ i d’un tractat sobre els coneixements de càlcul que havien de tenir els escribes i els funcionaris Fou també traductor i comentarista d’Euclides, de Diofant i de Ptolemeu
adjunt d’un element en un determinant
Matemàtiques
Coeficient d’un element d’un determinant en el desenvolupament del determinant.
Per exemple, en un determinant de tercer ordre els adjunts d' a 11 i a 12 són
teorema de Taylor
Matemàtiques
Teorema que dóna el desenvolupament en sèrie d’una funció f(x), fixat un punt a.
Si f x és una funció d’una variable real i derivable n vegades, la fórmula que expressa el teorema de Taylor és Els n +1 primers sumands d’aquesta expressió són coneguts com a polinomi de Taylor de grau n , per a f en el punt a , mentre que el terme R n+1 a x és anomenat resta Aquest terme compleix la següent condició d’aproximació És, per tant, un infinitèsim d’ordre superior a x-a n , i pot ésser expresat per qualsevol de les dues maneres següents per a algun t ∈ a,x , per a algun t ∈ a,x En el cas que f n⁺ 1 es pugui integrar en a,x , hom té l’expressió integral de la resta La…
nombres de Bernoulli
Matemàtiques
Nombres racionals Bn que apareixen com a coeficients dels termes, per a n parell de la forma
en el desenvolupament en sèrie de potències de la funció Així, B 1 = 1/6, B 2 = -1/30, B 3 = 1/42, etc Alguns autors anomenen nombres de Bernoulli els coeficients B n de x n / n en el desenvolupament de MacLaurin de x / e x -1, de què resulta B 0 = 1, B 1 = -1/2, B 2 = 1/6, B 4 = -1/30, B 6 =1/92, … i B 2 n +1 =0 Hom empra els nombres de Bernoulli en fórmules d' integració numèrica i en càlcul de diferències finites
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- Pàgina següent
- Última pàgina