Resultats de la cerca
Es mostren 26 resultats
espiral de Cornu
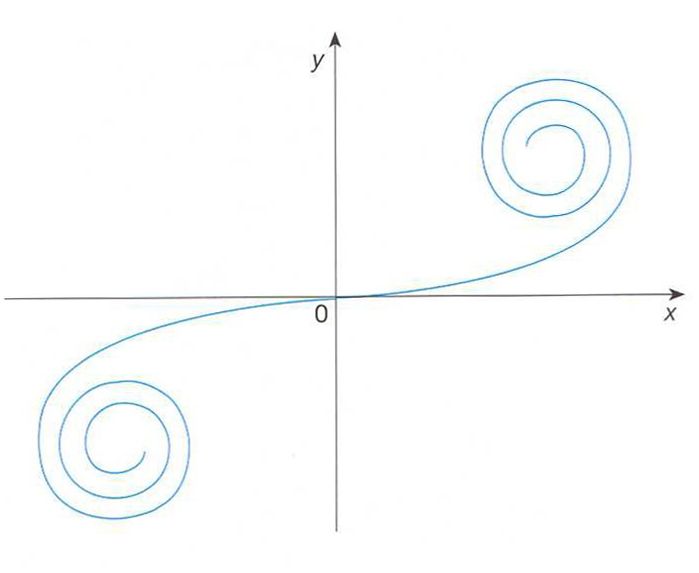
Espiral de Cornu
Matemàtiques
Corba plana l’equació intrínseca de la qual estableix la constància del producte del radi de curvatura per la longitud d’arc
.
És anomenada també clotoide L’espiral de Cornu té importància en la determinació d’intensitats en els fenòmens d’interferència
funció primitiva d’una funció
Matemàtiques
Donada una funció f(x), funció F(x) tal que F´(x)=f(x) (on F´(x) és la derivada de la funció F(x)).
Hom diu aleshores que F x és la funció primitiva o, simplement, la primitiva, de f x Les primitives d’una funció són obtingudes mitjançant la determinació de la integral indefinida d’aquesta, F x =∫ x a f t
transportador
transportador
Disseny i arts gràfiques
Matemàtiques
Cercle o semicercle graduat, de metall, plàstic, paper, etc, emprat per a mesurar i dibuixar angles sobre un paper.
En són modificacions els aparells usats amb la mateixa finalitat determinació d’angles en l’artilleria —com el transportador de Pfeiffer— i en topografia, que molts cops són complementats amb l’adaptació de nònius per a millorar la precisió de les mesures
hessià | hessiana
Matemàtiques
Dit de la matriu o del seu determinant formats per les derivades de segon ordre d’una funció de diverses variables.
Per exemple, la hessiana de f x , y = x 2 - 2 xy 2 és L’estudi dels valors de la matriu hessiana és important en la determinació de punts singulars i extrems de funcions de diverses variables Rep el seu nom del matemàtic LO Hesse
funció multiforme
Matemàtiques
Funció que assigna diverses imatges a cada element del domini de definició.
En són exemple les funcions trigonomètriques inverses arc sin1 = {π/2, π/2+2π, π/2+4π,,π/2+2 n π,} Les funcions multiformes no són, en el sentit estricte del terme funcions , sinó correspondències Una funció multiforme esdevé una funció quan hom n'escull una branca o determinació per exemple, la funció Arc sin x és la branca de la funció multiforme arc sin x definida en restringir a 0,2π el recorregut d’aquesta
Viktor Valentinovič Novožilov
Economia
Matemàtiques
Economista i matemàtic soviètic.
Professor a les universitats de Kíev, Rostov i Leningrad, en la qual substituí Nemčinov A partir del 1939 aparegueren els seus treballs sobre programació en la determinació del procés de producció òptim En l’obra Procediments per a la mesura de les despeses i els seus resultats en una economia socialista per determinar l’eficàcia de les noves tècniques 1958 introdueix elements com l’escassetat i l’eficàcia per a seleccionar les inversions que cal dur a terme Una gran part de les seves aportacions, però, no foren difoses fins al reconeixement de les tesis sobre l’assignació de…
mètode de Montecarlo
Matemàtiques
Mètode estadístic pel qual, mitjançant un mostreig artificial (que en general utilitza successions de xifres aleatòries), hom arriba a estimar la probabilitat que un procés real tingui lloc.
L’ús d’un mostreig artificial o procés de simulació , que actualment és facilitat per la utilització d’ordinadors, evita el mètode analític de comptabilitzar totes les dades reals que concorren en el procés analitzat i que, a causa de llur quantia i aleatorietat, desborden les possibilitats de comptabilització El mètode de Montecarlo fou perfeccionat entre els anys 1950 i 1960, i té com a antecedent històric l’estimació feta per GBuffon, l’any 1773, de les xifres decimals del nombre pi π El mètode ha estat utilitzat amb èxit en física nuclear determinació de les dimensions…
rectificació
Matemàtiques
Determinació de la longitud d’una corba o d’un arc d’aquesta.
Hom pot provar que la rectificació d’una circumferència és impossible de fer gràficament mitjançant el regle i el compàs
condició de Neumann
Matemàtiques
En la determinació d’una funció u que satisfaci l’equació de Laplace .
definida en una regió R del pla i tal que u sigui regular i contínua en R i en la seva frontera F , condició consistent a considerar coneguda la derivada normal du / dn de la funció u damunt la frontera F problema de Dirichlet
allisatge
Matemàtiques
Conjunt de mètodes per al tractament de dades estadístiques de tipus cronològic o sèries temporals, que tenen per objecte fer previsions a curt termini basades en les dades anteriors.
Hom tracta de separar la fluctuació aleatòria de la llei subjacent del fenomen, allisant els valors històrics anteriors La més emprada és la tècnica anomenada de les mitjanes mòbils , que pren com a previsió la mitjana aritmètica de les N darreres dades Hom pot veure fàcilment que S t +1 = S t + X t — X t-N /N Si es tracta, p ex, de preveure les vendes d’un producte per al més següent t+ 1, hom pren la mitjana dels darrers dotze mesos, amb la qual cosa hom suposa que s’eliminaran les variacions aleatòries El mètode de l' allisatge exponencial representa una elaboració de l’anterior que…