Resultats de la cerca
Es mostren 21 resultats
diàmetre
Matemàtiques
Línia que divideix per la meitat un sistema de cordes paral·leles d’una corba.
diàmetre
Matemàtiques
Corda que passa pel centre d’una figura (un cercle, una secció cònica, una esfera).
graf de Petersen
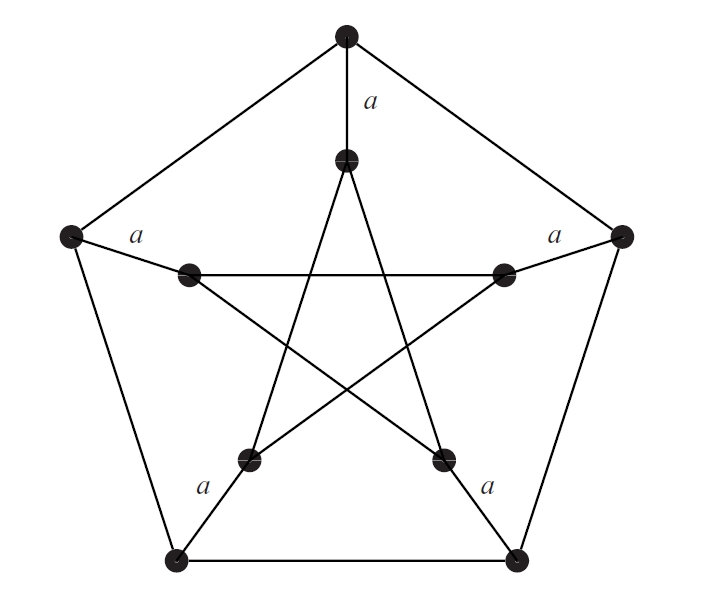
graf de Petersen
Matemàtiques
Graf 3-regular, d’ordre 10, que té diàmetre 2.
A més, és el graf 3-regular de diàmetre 2 amb el nombre més gran de vèrtexs El graf de Petersen és un graf vèrtex-transitiu amb nombre cromàtic 4, que no és de Cayley ni hamiltonià
semicircumferència
Matemàtiques
La meitat d’una circumferència.
És l’arc de circumferència que té per corda el diàmetre
digraf de Kautz
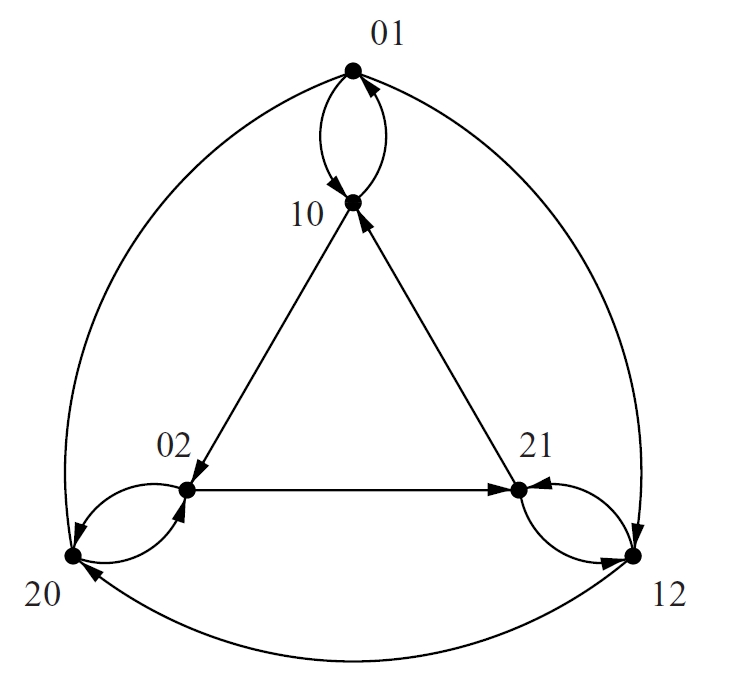
digraf de Kautz
Fototeca.cat
Matemàtiques
Digraf K(d, D) que té per conjunt de vèrtexs el de totes les paraules de longitud D que es poden formar amb els d + 1 símbols diferents d’un alfabet, de manera que dos símbols consecutius sempre siguin diferents.
Una paraula és adjacent respecte a una altra si la primera sense el símbol inicial és igual a la segona sense el símbol final El digraf de Kautz K d , D té diàmetre D
sòlid de revolució
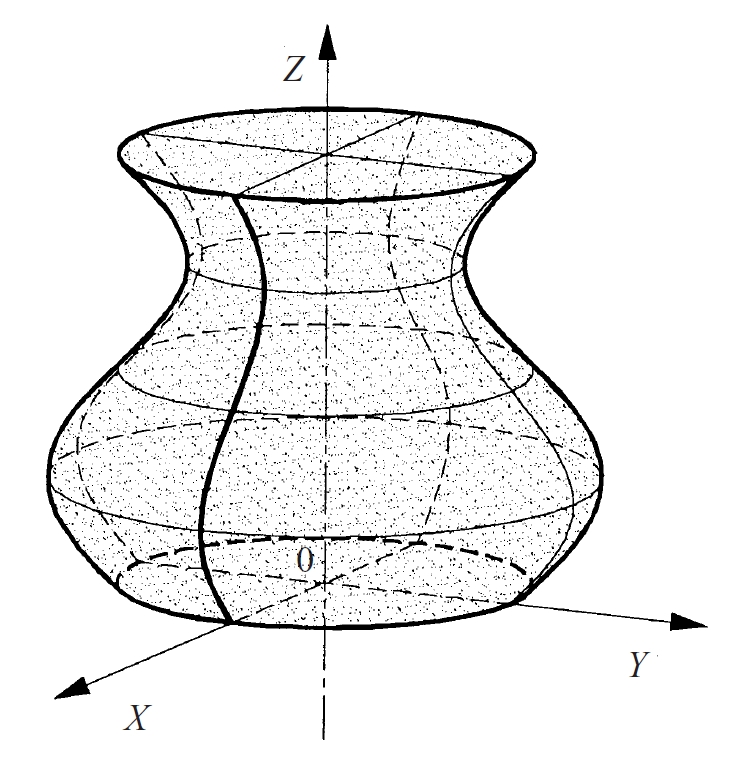
sòlid de revolució
Matemàtiques
Cos limitat per una superfície de revolució, que hom obté per la rotació d’una línia entorn d’un eix.
Així, l’esfera és el sòlid engendrat per un cercle que gira entorn d’un diàmetre el con de revolució és engendrat per una recta o un segment que talla l’eix al voltant del qual gira
fletxa
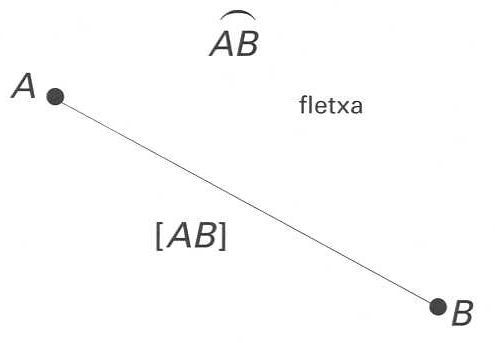
Fletxa d’un arc de corba AB
©
Matemàtiques
En un arc de corba AB, segment que uneix el centre de l’ar c AB amb el centre de la corda [AB].
Si AB és un arc d’una circumferència, la fletxa és situada sobre el diàmetre perpendicular a la corda AB , i la seva longitud és l = r 1—cosα/2, on r és el radi de la circumferència i α l’angle determinat pels diàmetres subtendits pels extrems de l’arc
pi
Matemàtiques
Lletra grega, inicial del mot grec περιφέρεια (‘circumferència’)..
És adoptada per a representar la raó constant que existeix entre la longitud de la circumferència i el seu diàmetre longitud de la circumferència, 2πR àrea del cercle, πR 2 àrea de l’esfera, 4πR 2 volum de l’esfera, L’ús d’aquesta llegra grega per a designar la relació entre la longitud de la circumferència i el seu diàmetre es remunta solament al s XVII, i es generalitzà a partir de la publicació de l’obra d’Euler Introductio in analysim infinitorum el mateix Euler i JBernoulli usaren P i c , respectivament, com a símbol representatiu A Egipte hom havia fet…
antípoda
Matemàtiques
Cadascun dels dos punts que són els extrems oposats del diàmetre d’una esfera.