Resultats de la cerca
Es mostren 10 resultats
Lev Sem’onovič Pontr’agin
Matemàtiques
Matemàtic rus.
Cec des de catorze anys, es graduà a la Universitat de Moscou el 1929, on tingué càrrecs acadèmics Féu recerques en topologia algèbrica, camp en el qual descobrí una llei general de dualitat Entre les seves nombroses publicacions destaca la dedicada als grups topològics 1938 Des dels anys cinquanta es dedicà sobretot a problemes de matemàtica aplicada Membre de l’Acadèmia Soviètica de les Ciències 1959, rebé nombrosos guardons, entre els quals el premi Lenin 1962 El 1970 fou elegit vicepresident de la Unió Internacional de Matemàtics
Curtis Tracy McMullen
Matemàtiques
Matemàtic nord-americà.
Es graduà l’any 1980 pel Williams College de Massachusetts i es doctorà l’any 1985 per la Universitat de Harvard Després de realitzar estudis postdoctorals ha estat professor a les universitats de Princeton 1987-90, Berkeley 1990-97 i, des del 1997, Harvard Ha treballat en el camp de la dinàmica complexa, una branca de la teoria del caos, demostrant el caràcter hiperbòlic d’una part del “grup Mandelbrot” Ha rebut el premi Salem 1991 i la Medalla Fields 1998 L’any 2007 fou elegit membre de l’Acadèmia Nacional de Ciències
perspectiva cavallera
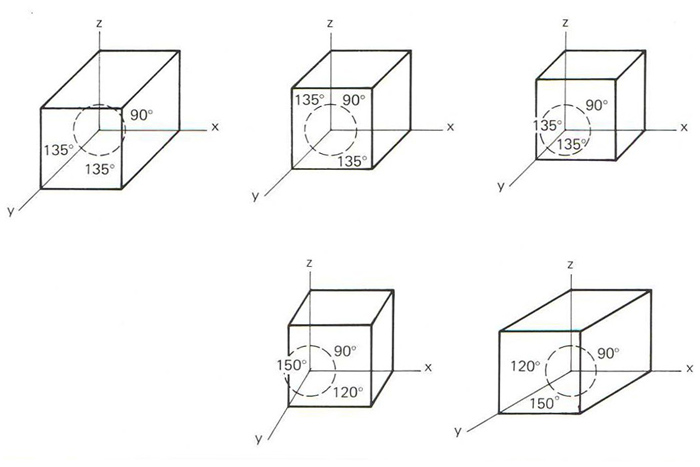
Representació d’un cub amb diferents reduccions i angles
© fototeca.cat
Art
Disseny i arts gràfiques
Matemàtiques
Projecció cilíndrica obliqua d’un cos sobre el pla de projecció (pla del quadre).
En aquest cas el pla del quadre és el mateix pla coordenat OXZ, i per això les rectes paralleles als eixos OZ i OX es projecten en llur veritable magnitud L’eix Y és projectat en el quadre amb una direcció dependent de la que tinguin les projectants, i sofreix, per tant, la reducció Per a les representacions en aquest sistema, caldrà conèixer la reducció de l’eix Y i el valor de l’angle XOY o YOZ, que oscillarà entre 0º i 360º aquesta relació serà constant per a totes les línies paralleles a l’eix Y L’angle que forma l’eix Y amb l’eix X podria ésser elegit indistintament, però evitant els…
teorema de la integral de Cauchy
Matemàtiques
Teorema relatiu a la integració en el camp complex que afirma que, per a tota funció f(z), de variable z complexa, holomorfa en un recinte simplement connex D, i per a qualsevol trajectòria tancada C continguda en D, es verifica: 72185.
Hom pot també enunciar aquest teorema dient que, en les condicions anteriors, la integral de f z entre dos punts de D és independent del camí d’integració elegit, sempre que aquest camí sigui contingut en D Aquest teorema és fonamental per a l’estudi de les funcions de variable complexa i dóna lloc a la teoria de la integració per residus integral Una aplicació immediata és la integral de Cauchy , mitjançant la qual hom pot expressar el valor d’una funció regular f z i de les seves derivades en un punt qualsevol a interior a un contorn al llarg de C , mitjançant les…
Joan Girbau i Badó
Matemàtiques
Matemàtic.
Estudià ciències matemàtiques a la Universitat de Barcelona 1959-64 Després d’ocupar diverses places de professor en aquesta universitat, entre el 1970 i el 1972 es traslladà a París, on feu els primers treballs de recerca sota la direcció d’André Lichnerowicz Catedràtic de la Universitat Autònoma de Barcelona des del 1976, treballà en diverses recerques relacionades amb la geometria diferencial, especialment la cohomologia de les varietats complexes i la teoria de les foliacions holomorfes Del 1986 al 1990 presidí la Societat Catalana de Matemàtiques L’any 1990 fou elegit membre…
nombre enter
Matemàtiques
Nombre que determina quantitats no fraccionables en parts més petites que la unitat.
La manera més simple d’introduir els nombres enters, positius i negatius, és imaginar una escala gràfica en la qual, a partir d’un punt elegit com a origen i designat amb el nombre zero , que no és positiu ni negatiu, hom senyala segments iguals en un sentit i en l’altre, designats amb els nombres naturals successius 1, 2, 3, , als quals hom afegeix, per tal de distingir els sentits, el signe + o el signe - Des d’aquest punt de vista, hom pot dir que un nombre enter és un nombre natural precedit d’un signe +o- Aquesta manera d’introduir els nombres enters, que és molt útil des…
superfície
Matemàtiques
Conjunt de punts de l’espai que poden ésser determinats per dos paràmetres.
La manera més simple de determinar una superfície és donar una o més equacions del tipus z = f x,y Elegit un punt x,y en el domini de definició de la funció f , aquesta funció o aquestes funcions donen els valors de z , que, juntament amb x,y , són les coordenades cartesianes dels punts de la superfície Les funcions que donen la superfície esfèrica són , on el signe + correspon a l’hemisferi superior, i el signe - a l’hemisferi inferior L’equació z = ax + by + c correspon al pla o superfície plana Sovint és difícil, o impossible, d’expressar una superfície per mitjà de les…
Abraham De Moivre
Matemàtiques
Matemàtic anglès d’origen francès.
Estudià a les universitats de Sedan, Saumur i París Després de la revocació de l’edicte de Nantes es traslladà a Anglaterra per tal de fugir de la persecució desencadenada a França contra els hugonots Ja a Anglaterra, l’astrònom EHalley presentà el seu treball “Specimen” 1967 a la Royal Society, de la qual fou elegit membre dos anys més tard La majoria dels seus treballs foren publicats en les Philosophical Transactions Arran de la polèmica entre Newton i Leibniz sobre la invenció del càlcul, formà part de la comissió que estudià el problema El seu primer estudi sobre…
Carlos Ibáñez e Ibáñez de Ibero

Carlos Ibáñez e Ibáñez de Ibero
© Fototeca.cat
Història
Militar
Matemàtiques
Matemàtic i militar.
El 1839 ingressà a l’acadèmia d’enginyers de l’exèrcit Publicà, amb Joan Modet, un Manual del pontonero 1853 Aquell mateix any fou membre de la comissió que havia de fer el mapa de l’Estat espanyol i inicià, així, els seus notables treballs geodèsics Feu construir, sota la seva direcció, a París, un aparell per a mesurar bases geodèsiques, que fou consultat pel govern egipci fou elegit membre de l’Institut Egipci Fou nomenat cap del primer districte geodèsic cadastral, que comprenia aleshores el País Valencià i les Illes Balears El 1864 publicà Estudio sobre la nivelación…
nombre real
Matemàtiques
Cadascun dels nombres que hom pot obtenir en mesurar magnituds contínues.
Hom obté el conjunt dels nombres reals completant el conjunt dels nombres racionals amb tots els nombres irracionals que poden ésser representats sobre la recta, tals com etc La manera més simple d’introduir teòricament i d’utilitzar en la pràctica els nombres reals és per mitjà de llur expressió decimal Tot nombre real és expressat en forma decimal amb infinites xifres que, en el cas dels nombres irracionals, no es repeteixen periòdicament Això suposa que per a definir un nombre real cal donar una llei que permeti d’obtenir tantes xifres decimals com hom vulgui A la pràctica, però, hom pren…