Resultats de la cerca
Es mostren 17 resultats
papir de Moscou
Matemàtiques
Papir del 1800 aC escrit en hieràtic.
Conté 19 problemes matemàtics, quatre dels quals fan referència a la geometria La seva importància radica en el fet que un d’aquests problemes conté el càlcul del tronc de piràmide, i l’algorisme que hom utilitza és absolutament correcte Cal esperar quinze segles per trobar un altre document amb aquesta fórmula o algorisme ℕdesigna el conjunt dels nombres naturals El conjunt ℕdels nombres naturals és la intersecció de tots els conjunts inducttius, és a dir, és el més petit dels conjunts inductius i conté 0 = 0, 1 = 0 ∪{0}, 2 = 1 ∪{1}, , n + 1 = n ∪{ n }, que són els nombres…
papir d’Akhim
Matemàtiques
Papir escrit en grec entre els segles V i VIII aC.
És molt semblant al papir de Rhind, la qual cosa posa de manifest que les tècniques del papir de Rhind es mantingueren durant segles Hom el coneix també amb el nom de papir del Caire
màquina de Turing
Matemàtiques
Màquina formada per una cinta il·limitada, dividida en cel·les, i per una capsa negra amb un cap lector.
Procedeix de la següent manera elemental A cada cella de la cinta hom pot escriure un 0 o un 1 Aleshores, la màquina de Turing, segons l’estat intern de la capsa negra i del símbol que llegeix el cap lector, pot pendre una de les cinc decisions següents 1, escriure un zero a la cella llegida pel cap lector, esborrant abans el que pugui haver-hi escrit 2, escriure un 1 a la cella, esborrant abans el que pugui haver-hi escrit 3, donar un pas cap a la dreta 4, donar un pas cap a l’esquerra 5, aturar-se Una màquina de Turing és, doncs, una matriu com ara Aquesta matriu…
projecció fitada
Matemàtiques
Sistema de projecció que utilitza només com a pla de projecció el pla horitzontal i substitueix el vertical per un nombre.
Aquest nombre, que indica la distància del punt al pla, és escrit al costat de la projecció horitzontal en una unitat determinada El pla de projecció rep el nom de pla de comparació i els nombres escrits amb cada projecció són anomenats fites Així, un punt és determinat per la seva situació a l’espai respecte al pla de comparació i la seva fita Per distingir els punts que hi ha a sobre del pla de comparació dels que hi ha a sota, els primers porten la fita positiva i els segons negativa
Johannes von Neumann
Matemàtiques
Matemàtic hongarès naturalitzat nord-americà.
Fou un dels pocs matemàtics moderns que reeixí alhora en l’estudi de qüestions de teoria pura teoria de conjunts continuant les investigacions de Zermelo, àlgebra topològica, teoria dels jocs anomenats estratègics , formulació axiomàtica de la mecànica quàntica, etc i en la matemàtica aplicada calculadors electrònics amb “memòria” contenint no sols les dades numèriques d’un problema, sinó també les instruccions que permeten de resoldre'l, com l’EDVAC del 1945, i especialment les màquines autoreproductores, que imiten procediments naturals apresos de la genètica, ideades l’any…
hexadecimal
Matemàtiques
Electrònica i informàtica
Dit del sistema de numeració de base setze.
És emprat en informàtica per a transciure un nombre format per moltes xifres binàries 1 i 0 Hom agrupa els bits de 4 en 4, i per a representar les xifres de més enllà del 9 són emprades les lletres majúscules A, B, C, D, E, F Així, el nombre 0101 1010 1110 1111, de 16 bits, és escrit 5AEF De fet, és un sistema d’escriptura condensada i no de codificació Sistema hexadecimal xifra hexadecimal representació binària valor decimal 0 0000 0 1 0001 1 2 0010 2 3 0011 3 4 0100 4 5 0101 5 6 0110 6 7 0111 7 8 1000 8 9 1001 9 A 1010 10 B 1011 11 C 1100 12 D 1101 13 E 1110 14 F 1111 15 <
nombre complex
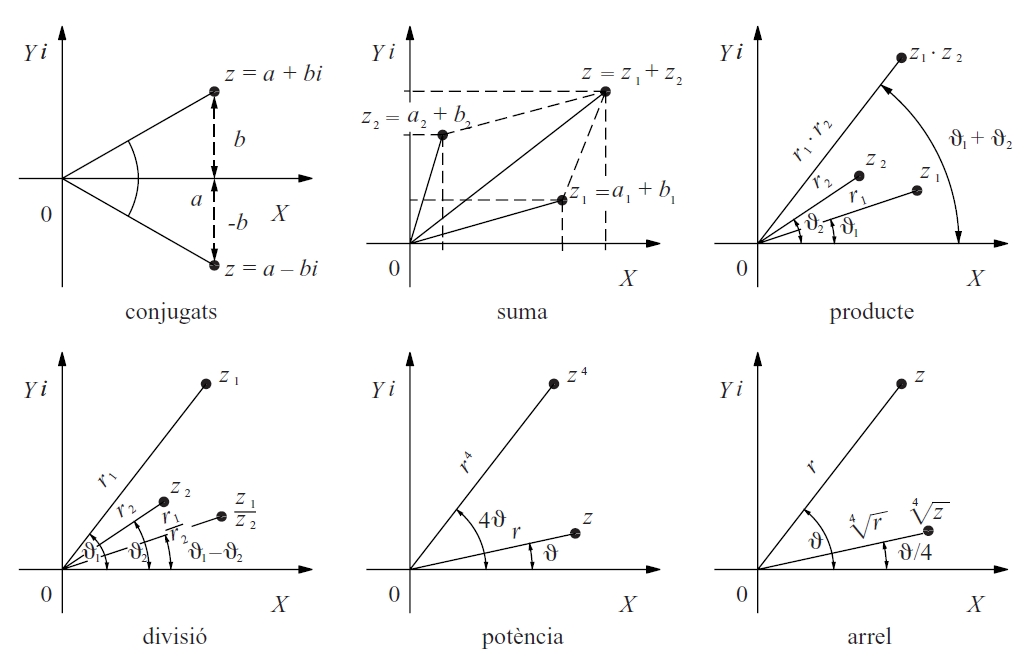
Nombres complexos
Matemàtiques
Nombre que pot ésser expressat com a suma d’un nombre real i d’un nombre imaginari.
Hom construeix el conjunt ℂ dels nombres complexos afegint al conjunt dels nombres reals un nombre nou, no real, que hom representa per una i , i que és definit formalment per la propietat que el seu quadrat és -1 Hom estén a aquest conjunt ℂ les operacions d’addició i de multiplicació amb totes les propietats que tenen entre nombres reals Cada nombre complex pot ésser escrit en forma de polinomi de primer grau en i , a + bi , i pot ésser representat geomètricament en el pla prenent a i b com a coordenades en un sistema cartesià ortogonal pla d'Argand-Gauss Aquesta…
teorema de Rouché-Frobenius
Matemàtiques
Teorema que permet la classificació dels sistemes lineals d’equacions.
Donat un sistema no homogeni de m equacions lineals amb n incògnites, escrit en forma matricial A x = b , b ≠ 0 , on A és la matriu de coeficients del sistema, b la columna dels termes independents i x la columna de les incògnites, el sistema és compatible és a dir, que té solucions si el rang de A és igual al rang de la matriu ampliada A , b matriu Si aquest rang és igual al nombre d’incògnites, aleshores es tracta d’un sistema compatible determinat o sia, amb solució única, però si el rang és menor que el nombre d’incògnites, es tracta d’un sistema compatible indeterminat amb infinites…
equació diferencial
Matemàtiques
Equació funcional (en el sentit que les incògnites són funcions) on apareixen les derivades de la funció incògnita.
Si la funció és d’una sola variable, l’equació és una equació diferencial ordinària Per tal que aquesta definició, molt general, no inclogui certes classes d’equacions especials com és ara les equacions diferencials en diferències f ´ x = f x + h , hom precisa que la funció incògnita i les seves derivades tan sols poden ésser sotmeses a operacions algèbriques El tipus general d’equació diferencial és escrit F t,x,x´,,x n = 0 Hom defineix l' ordre d’una equació diferencial com el de la màxima derivada que apareix en l’equació Si F té forma polinòmica, hom parla de grau de l’…
computable
Matemàtiques
Tipus de relació R ⊑ ℕn en la qual la seva funció característica 1R és computable.
Una funció f A ⊑ ℕ n → ℕ és computable si, i només si, existeix un algorisme formal, com ara una màquina de Turing que la computa Quan diem, però, que una funció k -ària f A ⊑ ℕ k → ℕ és computable per mitjà d’una màquina de Turing OOO La idea és la següent a la cinta de la màquina colloquem n 1 + 1 uns seguits d’un zero, després d’n 2 + 1 uns seguits d’un zero,, després n k + 1 uns seguits d’un zero i colloquem la màquina en estat intern q 0 i amb el cap lector en el zero que hi ha al darrere dels darrers n k + 1 uns La resta de la cinta és plena de zeros El zero significa que a la cella…