Resultats de la cerca
Es mostren 4 resultats
Berthold Schweizer
Matemàtiques
Matemàtic alemany, naturalitzat nord-americà des del 1937.
Deixeble del prestigiós matemàtic Karl Menger, fou professor a les universitats de Califòrnia, Arizona i Massachusetts Amherst Impartí cursos en diverses universitats europees i publicà un gran nombre de treballs de recerca Especialista en àlgebra de funcions i en equacions funcionals, conjuntament amb Abe Sklas, fou fundador de la teoria dels espais mètrics probabilístics idea introduïda per Menger, disciplina d’un extraordinari interès científic
Jakob Steiner
Matemàtiques
Matemàtic suís.
Analfabet fins a 14 anys, estudià amb Pestalozzi, i després a Heidelberg i Berlín, on fou nomenat professor extraordinari el 1934 Féu recerques importants en geometria superfícies cúbiques i de quart ordre i geometria projectiva, amb els seus mètodes sintètics Publicà Systematische Entwicklung der Abhängigkeit geometrischer Gestalten von Einander ‘Desenvolupament sistemàtic de la interdependència de les figures geomètriques’, 1932 i pòstumament 1882 aparegueren les seves obres completes Ideà, entre altres, el teorema que du el seu nom
funció exponencial
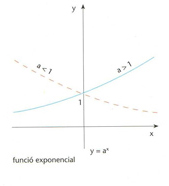
Funció exponencial
© Fototeca.cat
Matemàtiques
Funció contínua f
:ℝ→ℝ +
-{0} que satisfà f
( x
+ x
’) = f
( x
) f
( x
’), per a tot parell x,x
’∈ℝ, i f
(1)= a
, essent a
un nombre real concret que la caracteritza, anomenat base
.
És denotada per l’assignació x → a x És la funció inversa de la funció logarítmica de base Hom empra, especialment, la funció exponencial que té per base el nombre e aquesta és la inversa de la funció logarítmica neperiana ln e x = e l n x = x Quan hom no especifica la base, hom parla de funció exponencial o simplement d’exponencial, tot sobreentenent que es tracta de la funció exponencial de base e , i la nota e x o exp x Té la propietat d e x / dx = e x , i admet el desenvolupament en sèrie Aquesta sèrie convergeix també en el cos ℂ, la qual cosa permet de definir-hi la funció…
estadística
Matemàtiques
Ciència, mètode, tècniques, operació d’anàlisi matemàtica, que permeten d’estudiar numèricament amb el màxim de precisió els fenòmens col·lectius incompletament coneguts.
Molt abans que les dades provinents d’observacions poguessin ésser estudiades rigorosament i científicament, els estats havien organitzat, amb més o menys cura, la recollecció pretesament exhaustiva de dades amb fins diversos, principalment per a les lleves militars i els imposts És ben conegut el cens ordenat pels romans l’any 0 hom coneix, també l’existència d’elaboració de censos fa uns 4 000 anys a la Xina, i la Bíblia n'esmenta diversos en el llibre dels Nombres L’estadística permet a l’administració de conèixer la situació de les persones i dels béns que hi ha sota llur jurisdicció…