Resultats de la cerca
Es mostren 5 resultats
pla complex
Matemàtiques
Pla de ℝ 2
obtingut mitjançant la identificació dels punts < x
, y
> amb els nombres complexos x
+ iy
.
Aquest pla rep també el nom de pla de Gauss o de Gauss-Argand Un punt z = < x , y > admet una representació en coordenades polars i, per tant, z = ρ ⋅ cos θ + i ⋅ sin θ que, d’acord amb la identitat d’Euler, hom escriu z = ρ ⋅ e i⋅θ Aquesta expressió permet de calcular amb facilitat les potències dels nombres complexos i extreure'n les seves arrels n -èsimes Resulta aleshores que la fórmula de Moivre s’expressa
autòmat finit indeterminista
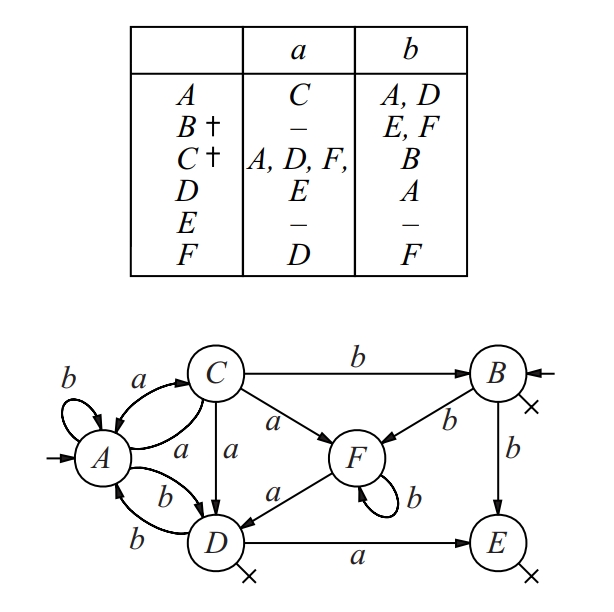
autòmat finit indeterminista
Matemàtiques
Estructura de la forma M = (Q, ∑, δ, I, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet anomenat d’entrada; δ : 2Q ⨉ ∑* → 2Q és la funció de transició que satisfà ∀P1, P2 ⊂ Q, ∀x, y∈∑*: δ(∅, x) = ∅, δ(P1, λ) = P1, δ(P1 ∪ P2, x) = δ(P1, x) ∪ δ(P2, x), δ(P1, xy) = δ(δ(P1, x)y), essent xy la concatenació de x i de y i ∑* el conjunt de paraules; I ⊂ Q és el conjunt d’estats inicial; F ⊂ Q és el conjunt d’estats finals o acceptadors.
Usualment un autòmat finit indeterminista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si q j ∈ δ q i , a S’indiquen els esstats inicials amb fletxes i els finals amb una creu Els llenguatges acceptats pels autòmats finits indeterministes són els mateixos que els reconeguts pels finits deterministes regulars L’avantatge dels indeterministes enfront dels deterministes és la facilitat de maneig i de construcció
mètode de Montecarlo
Matemàtiques
Mètode estadístic pel qual, mitjançant un mostreig artificial (que en general utilitza successions de xifres aleatòries), hom arriba a estimar la probabilitat que un procés real tingui lloc.
L’ús d’un mostreig artificial o procés de simulació , que actualment és facilitat per la utilització d’ordinadors, evita el mètode analític de comptabilitzar totes les dades reals que concorren en el procés analitzat i que, a causa de llur quantia i aleatorietat, desborden les possibilitats de comptabilització El mètode de Montecarlo fou perfeccionat entre els anys 1950 i 1960, i té com a antecedent històric l’estimació feta per GBuffon, l’any 1773, de les xifres decimals del nombre pi π El mètode ha estat utilitzat amb èxit en física nuclear determinació de les dimensions…
criptografia
Matemàtiques
Aplicació de tècniques matemàtiques que permeten xifrar i desxifrar missatges, de manera que només pugui ésser interpretat pel receptor al qual van adreçats.
Hi ha diferents estratègies per a xifrar la informació, però gairebé totes consisteixen a modificar algun paràmetre de la comunicació segons una seqüència pseudoaleatòria coneguda per l’emissor i pel receptor La seqüència és pseudoaleatòria en aquest sentit el receptor que desconeix la clau amb què ha estat generada interpreta que és del tot aleatòria, mentre que aquell que sí que la coneix pot reproduir la seqüència amb una certa facilitat El xifratge de la informació s’estén a tot tipus de comunicació que requereixi un cert grau de seguretat i als sistemes de radiodifusió de pagament La…
logaritme
Matemàtiques
Donat un nombre b, real, positiu i distint d’1 (anomenat base), i un nombre qualsevol n real i positiu, nombre a tal, que b, elevat a a, és igual a n, o sia, ba= n.
Hom l’anomena logaritme de base b de n , i el representa per log b n = a Les propietats fonamentals dels logaritmes són Els logaritmes constitueixen un instrument matemàtic que facilita i abreuja molts càlculs complicats Els més utilitzats correntment en el càlcul són els logaritmes decimals, vulgars o de Briggs , que són els logaritmes de base 10 i que hom representa amb els símbols log 1 0 , log o lg Per contra, en els càlculs diferencial i integral són utilitzats els logaritmes naturals o neperians , que són els logaritmes de base e , i hom els representa amb els símbols log e , ln o L…