Resultats de la cerca
Es mostren 15 resultats
focus
Matemàtiques
Punt la distància del qual a qualsevol dels punts d’una corba pot ésser expressada com una funció racional de les coordenades dels punts.
Aquesta definició mètrica de focus, que és una generalització dels focus de les còniques cònica, no permet, però, d’ésser estesa a una corba algèbrica qualsevol, i per aconseguir-ho cal passar a la definició projectiva de focus
paràbola
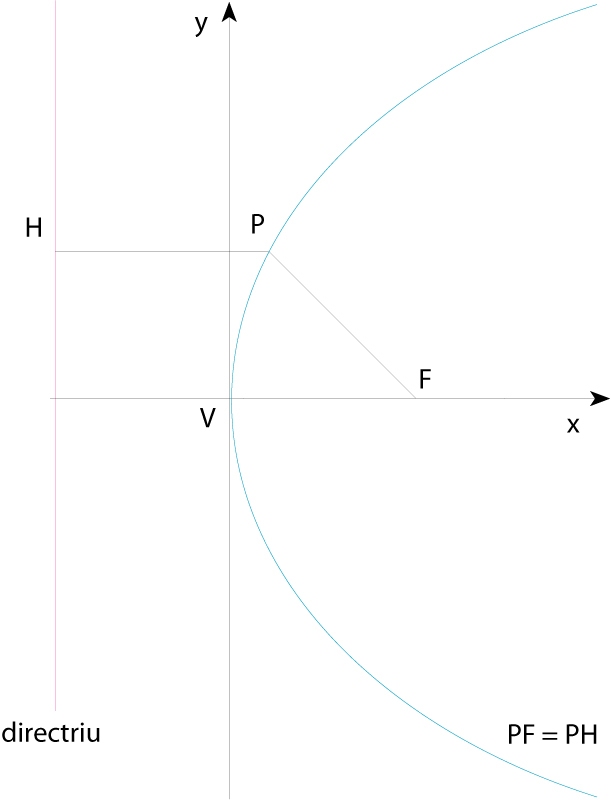
Paràbola (V vèrtex, F focus, P punt qualsevol de la paràbola)
© Fototeca.cat
Matemàtiques
Corba oberta, intersecció d’una superfície cònica amb un pla paral·lel a una de les generatrius.
Constitueix el lloc geomètric dels punts del pla que equidisten d’un punt el focus de la paràbola i d’una recta que no conté el punt la directriu de la paràbola Té un eix de simetria que és la recta perpendicular que passa pel focus i que talla la paràbola en un punt anomenat vèrtex Referida a l’eix de simetria i a la seva perpendicular pel vèrtex, l’equació de la paràbola és y 2 =2 px , on p és la distància entre focus i directriu, anomenada paràmetre de la paràbola Hom pot demostrar que la gràfica de tota funció polinòmica de segon grau y= ax 2 + bx+…
el·lipse
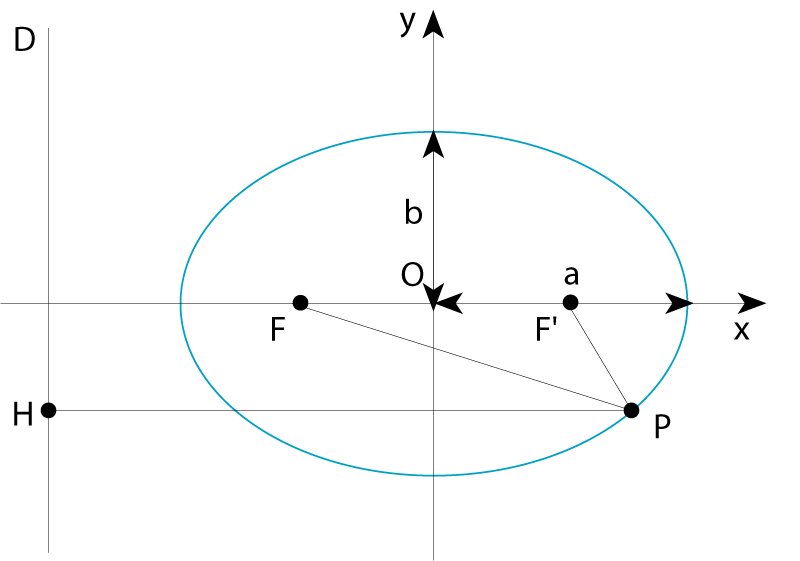
El·lipse de semieixos a i b; D és la directriu associada al focus F
© Fototeca.cat
Matemàtiques
Corba tancada que resulta de la intersecció d’una superfície cònica amb un pla que no és paral·lel a cap generatriu ni a l’eix d’aquella; és doncs, una cònica
.
La seva equació en coordenades cartesianes referides als seus dos eixos perpendiculars de simetria és x 2 / a 2 + y 2 / b 2 =1, a essent el semieix major i b el semieix menor L’ellipse és el lloc geomètric dels punts P del pla tals que la suma de llurs distàncies a dos punts fixos F i F ´, anomenats focus , és una quantitat constant, independent del punt P concret, igual al doble del semieix major, PF + PF ´=2 a és també el lloc geomètric dels punts P tals que el quocient de llurs distàncies a un punt fix, un dels focus, i a una recta fixa D , anomenada directriu…
radi vector
Matemàtiques
Vector que va des d’un origen o punt fix determinat (centre, pol, focus, etc) a un punt variable.
El radi vector d’una ellipse o d’una hipèrbola és definit com el que va des de qualsevol dels focus de la cònica fins a un punt variable d’aquesta
corba bipolar
Matemàtiques
Corba plana que pot ésser definida com el conjunt de punts les coordenades bipolars dels quals, respecte a dos focus F i F´, satisfan una determinada relació, anomenada equació bipolar de la corba.
P ex, l’ellipse és determinada pel fet que els seus punts satisfan r + r' = 2 a , essent a el semieix major i r i r' les distàncies dels punts als focus F i F'
perspectiva central
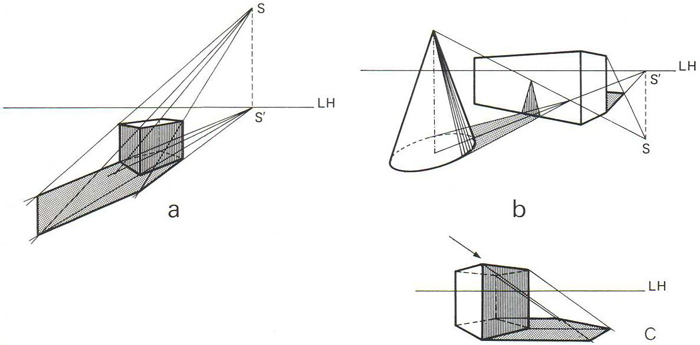
Ombra pròpia i ombra llançada projectades pel Sol (S) (projecció de la llum solar). LH essent la línia de l’horitzó i S’ el punt de fuga, quan és situat davant l’espectador (a), darrere l’espectador (b) i al costat de l’espectador (c)
© fototeca.cat
Art
Disseny i arts gràfiques
Matemàtiques
Sistema de representació les línies projectants del qual passen per un punt fix anomenat centre de projecció
o pol
.
Variants d’aquest tipus de perspectiva són la perspectiva cònica i la projecció de la llum el centre d’aquesta projecció és el focus o punt lluminós, que pot ésser a una distància finita dels cossos que illumina, i en aquest cas els raigs són divergents llum artificial , o infinita, i aleshores els raigs són parallels llum solar Ombres pròpies i ombres llançades projectades pel focus F projecció de llum artificial, F’ essent els punts de fuga © fototecacat
homofocal
Matemàtiques
Dit de les figures geomètriques que tenen els mateixos focus.
hipèrbole
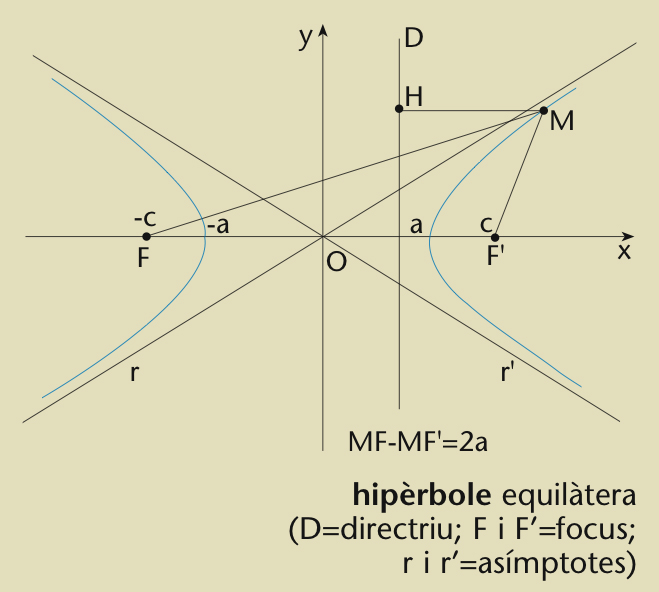
Hipèrbole equilàtera
© Fototeca.cat
Matemàtiques
Corba oberta, intersecció d’un con de revolució amb un pla que forma amb ’eix d’aquell un angle més petit que amb la generatriu.
Constitueix el lloc geomètric dels punts del pla tals que la diferència de llurs distàncies a dos punts fixos, anomenats focus , és una constant, simbolitzada habitualment per 2 a Té dos eixos de simetria i, referida a ells, la seva equació és x 2 / a 2 - y 2 / b 2 = 1, on i 2c és la distància entre els focus L’excentricitat e és c / a Les asímptotes són les rectes y = b / a x asímptota Quan a = b , la hipèrbola és anomenada equilàtera , i la seva equació referida a les asímptotes, que són perpendiculars, és y = k/ x la seva excentricitat és