Resultats de la cerca
Es mostren 7 resultats
Pierre Deligne
Matemàtiques
Matemàtic való.
Format a la Universitat de Brusselles i a París, és especialista en geometria algèbrica i en teoria dels nombres El 1974 demostrà la conjectura de Weil, formulada trenta anys abans, i el 1978 li fou atorgada la medalla Fields
Carl Friedrich Gauss
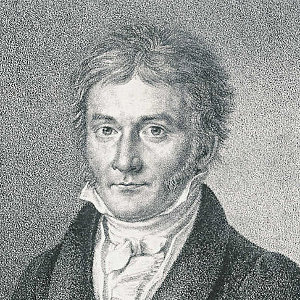
Carl Friedrich Gauss
Matemàtiques
Matemàtic alemany.
De família humil, extraordinàriament dotat per a les matemàtiques, pogué rebre ensenyament superior gràcies a la protecció del duc de Brunsvic, que l’envià a la Universitat de Göttingen Director de l’observatori i professor d’astronomia en aquella ciutat, hi residí fins a la mort, dedicat totalment a una fecunda tasca intellectual Els matemàtics li deuen aportacions transcendentals en la teoria dels nombres i en l’àlgebra noció de congruència i notació corresponent, sistematització de l’ús de demostració rigorosa del teorema fonamental de l’àlgebra, teoria de determinants , etc, qüestions…
contrast d’hipòtesi
Matemàtiques
Prova que consisteix en la realització d’experiències que permetin de determinar el valor d’una variable aleatòria definida en funció de la hipòtesi formulada en termes estadístics.
Prèviament hom ha d’estudiar la llei de probabilitat d’aquesta variable aleatòria per tal de fixar uns límits més enllà dels quals la probabilitat sigui negligible si el resultat de les experiències dóna per a la variable un valor comprès dins aquests límits, hom considera acceptable la hipòtesi H 0 , anomenada hipòtesi nulla , sense que això vulgui dir que és certa, sinó només que res no s’oposa a tenir-la per certa d’acord amb la informació obtinguda Altrament hom preferirà l’anomenada hipòtesi alternativa H 1 , única o diversa, diferent de la primera Cadascuna de les dues decisions…
teoria de nombres
Matemàtiques
Part de la matemàtica que estudia les relacions entre els nombres enters.
En la història de la teoria de nombres hom pot assenyalar dos grans períodes un que va des d’Euclides fins a Hilbert, i un altre que comença a partir de Hilbert Els primers tractats de teoria de nombres es troben en els Elements d’Euclides i en l' Aritmètica de Diofant d’Alexandria, i tracten, respectivament, de la divisibilitat en els racionals enters i de l’obtenció de solucions racionals i enteres d’algunes equacions algèbriques La figura més coneguda d’aquesta primera etapa és la del matemàtic francès Pierre de Fermat 1601-65, que conjecturà el famós gran teorema de Fermat encara avui no…
probabilitat
Matemàtiques
Concepte que permet d’expressar quantitativament el caràcter aleatori d’un esdeveniment o fenomen que hom creu que pot succeir.
El càlcul de probabilitats , branca de la matemàtica que presenta un gran nombre d’aplicacions científiques i tècniques, sorgí a França al s XVII amb els matemàtics B Pascal i P Fermat La motivació principal era l’estudi del guany esperat en els jocs d’atzar ruletes, daus, cartes, etc i, per tant, l’objectiu era el càlcul directe de la probabilitat utilitzant tècniques de combinatòria La noció de probabilitat en què hom es basava fou formulada l’any 1795 pel matemàtic francès P S Laplace de la següent manera “Si un fenomen pot produir un nombre de resultats diferents i igualment…
conjunt

Representació gràfica de la relació de pertinença i de les operacions d’unió i intersecció dels conjunts
© Fototeca.cat
Matemàtiques
Reunió d’objectes ben definits en la intuïció o en el pensament, considerada com una totalitat (Cantor).
Aquesta definició, des del punt de vista matemàtic, no és vàlida, i, així, en matemàtiques la noció de conjunt no és definida, i s’inclou dins del desenvolupament d’una teoria axiomàtica que eviti les paradoxes i contradiccions com les que, a començament del segle XX, posaren en qüestió no solament la teoria de conjunts, sinó bona part de la matemàtica Hom no defineix, doncs, ni conjunt, ni element, ni la relació de pertinença, i es conforma amb la idea intuïtiva del que signifiquen frases com Un conjunt és format per elements, o l’element 4 pertany al conjunt dels nombres naturals La…
matemàtica
Matemàtiques
Ciència que estudia les propietats dels nombres, de les figures, dels conjunts, de les operacions, de les funcions, etc.
Aquesta definició és força descriptiva, però incompleta, i per això diversos matemàtics han intentat de definir la matemàtica tot assenyalant-ne els trets més característics Així, segons B Russell, la matemàtica consisteix només en afirmacions tals com “si una proposició és veritable referida a un objecte, aleshores una altra proposició també ho és”, de manera que la matemàtica és aquell camp en què hom no sap mai de què parla ni si allò que diu és veritat o no Dins aquesta mateixa línia, H Poincaré diu que els matemàtics no estudien objectes, sinó relacions entre objectes no els interessa la…