Resultats de la cerca
Es mostren 46 resultats
Carl Friedrich Gauss
Carl Friedrich Gauss
Matemàtiques
Matemàtic alemany.
De família humil, extraordinàriament dotat per a les matemàtiques, pogué rebre ensenyament superior gràcies a la protecció del duc de Brunsvic, que l’envià a la Universitat de Göttingen Director de l’observatori i professor d’astronomia en aquella ciutat, hi residí fins a la mort, dedicat totalment a una fecunda tasca intellectual Els matemàtics li deuen aportacions transcendentals en la teoria dels nombres i en l’àlgebra noció de congruència i notació corresponent, sistematització de l’ús de demostració rigorosa del teorema fonamental de l’àlgebra, teoria de determinants , etc,…
teorema de Gauss
Física
Matemàtiques
Donat un camp vectorial A, per a tota regió de l’espai de volum V limitada per una superfície S, es compleix que: ∫∫sA·dS = ∫∫∫vdivA dV.
El primer terme de l’equació és el flux de A a través de S És anomenat també teorema de la divergència o d’Ostrogadskij En el cas d’un camp elèctric E , el teorema de Gauss pren la forma q essent-hi la càrrega total dins la regió limitada per S, i ε, la constant dialèctica del medi En el cas d’un camp magnètic B , el teorema de Gauss diu cosa que implica la inseparabilitat dels pols magnètics
campana de Gauss
Matemàtiques
Corba que té per equació cartesiana
.
En estadística representa la funció de distribució normal o de Gauss
enter de Gauss
Matemàtiques
Nombre complex de la forma a + bi, a i b essent-hi enters i .
El conjunt d’enters de Gauss, ℤ i , té estructura d’anell amb unitat
pla d’Argand-Gauss
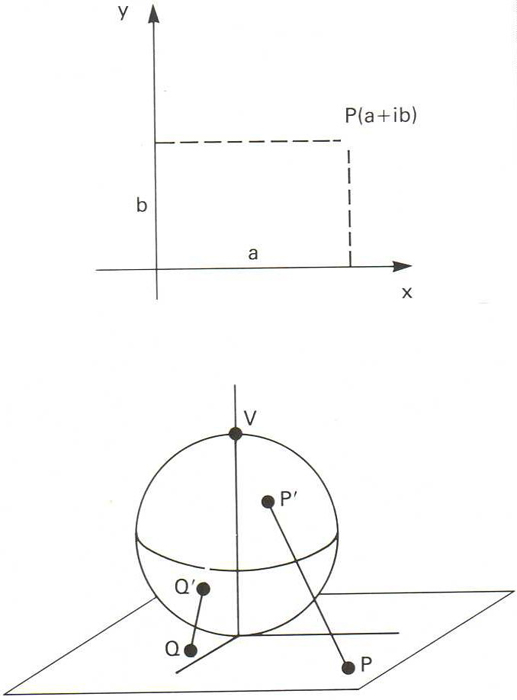
Representació del pla d’Argand-Gauss
© fototeca.cat
Matemàtiques
Pla on ha estat establert un sistema de coordenades cartesianes i en el qual és representat cada nombre complex a + bi per mitjà del punt de coordenades (a, b).
En aquesta representació tots els punts que tenen una o totes dues coordenades infinites són considerats com un mateix punt Per a fer intuïtiu el fet de considerar com un sol tots aquests punts hom utiliza la projecció estereogràfica del pla d’Argand-Gauss sobre una esfera tangent a l’origen de coordenades, de manera que tots els punts de l’infinit del pla van a parar al punt V de l’esfera
nombre primer de Gauss
Matemàtiques
Cadascun dels nombres primers que poden ésser expressats per la fórmula 22n + 1.
Gauss els emprà en estudiar les possibles divisions del cercle, i arribà a la conclusió que hom pot construir amb regle i compàs tot polígon regular amb un nombre primer 2 2 n + 1 de costats
mètode de racionalització de Gauss
Matemàtiques
Algorisme emprat en l’estudi dels espais vectorials que, donats uns vectors arbitraris, permet de deduir-ne efectivament els que són linealment independents i que, per tant, també són base del subespai que generen.
Hom aplica aquest mètode per a trobar el rang d’una matriu qualsevol no necessàriament quadrada, considerant cada fila de la matriu com un vector
llei normal
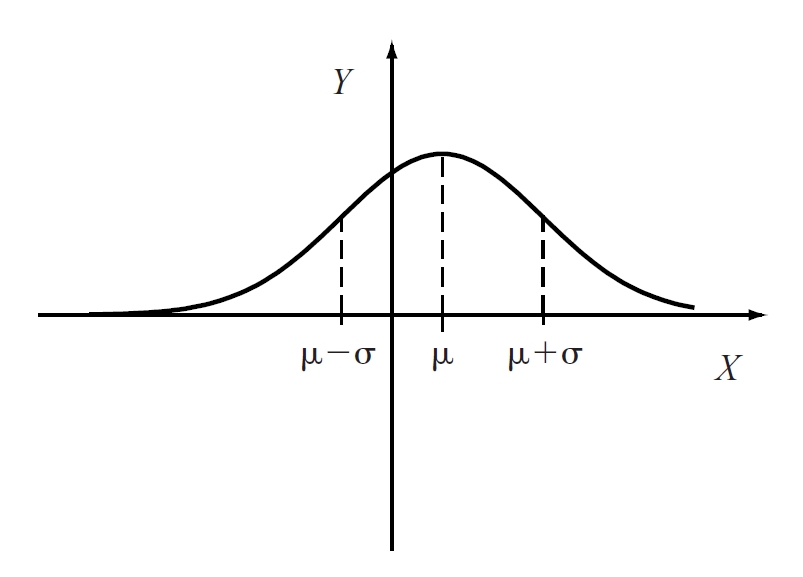
Llei normal de probabilitat de mitjana μ i desviació tipus σ
Fototeca.cat
Matemàtiques
Llei de probabilitat contínua i simètrica en la qual la mitjana, la moda i la mediana coincideixen i la funció de densitat té forma de campana de Gauss o corba normal.
Aquesta densitat depèn de dos paràmetres, la mitjana μ i la desviació típica σ En general, es caracteritza per N μ, σ i la seva funció de densitat val
pla complex
Matemàtiques
Pla de ℝ 2
obtingut mitjançant la identificació dels punts < x
, y
> amb els nombres complexos x
+ iy
.
Aquest pla rep també el nom de pla de Gauss o de Gauss-Argand Un punt z = < x , y > admet una representació en coordenades polars i, per tant, z = ρ ⋅ cos θ + i ⋅ sin θ que, d’acord amb la identitat d’Euler, hom escriu z = ρ ⋅ e i⋅θ Aquesta expressió permet de calcular amb facilitat les potències dels nombres complexos i extreure'n les seves arrels n -èsimes Resulta aleshores que la fórmula de Moivre s’expressa
Julius Wilhelm Richard Dedekind

Julius Wihelm Richard Dedekind
© Fototeca.cat
Matemàtiques
Matemàtic alemany, deixeble de Gauss.
Professor al politècnic de Zuric 1858 i a la Technische Hochschule de Brunsvic 1862-1912, ha estat un dels capdavanters de dos dels corrents bàsics que han donat origen i suport a la matemàtica moderna el formalista culminat en l’obra de Hilbert, que bandeja qualsevol possibilitat d’incloure un raonament basat en la intuïció dins l’edifici matemàtic, i el logicista Was sind und was sollen die Zahlen , ‘Què són i per a què serveixen els nombres', 1888, que pretén de situar la matemàtica com a branca particular de la lògica, elaborat fins a les darreres conseqüències per Russell Construí una…