Resultats de la cerca
Es mostren 7 resultats
mesura
Física
Matemàtiques
Unitat de mesura, habitualment amb exclusió de les de pes.
ajust
Matemàtiques
Operació estadística que consisteix a trobar la llei que resumeix, de la millor manera possible, la variació d’una variable aleatòria Y
en funció d’una altra variable X
, de la qual depèn.
Hom fa l’ajust a partir del coneixement de parells de valors x,y obtinguts observant una mostra, com la capacitat pulmonar i l’edat Deixant de banda l’ajust purament gràfic allisatge, habitualment hom pren una funció f x lineal, exponencial, polinòmica, etc i se suposa que y=f x +ε, on ε és un residu aleatori o soroll, i els paràmetres que defineixen la funció són determinats pel mètode dels mínims quadrats
hipèrbole
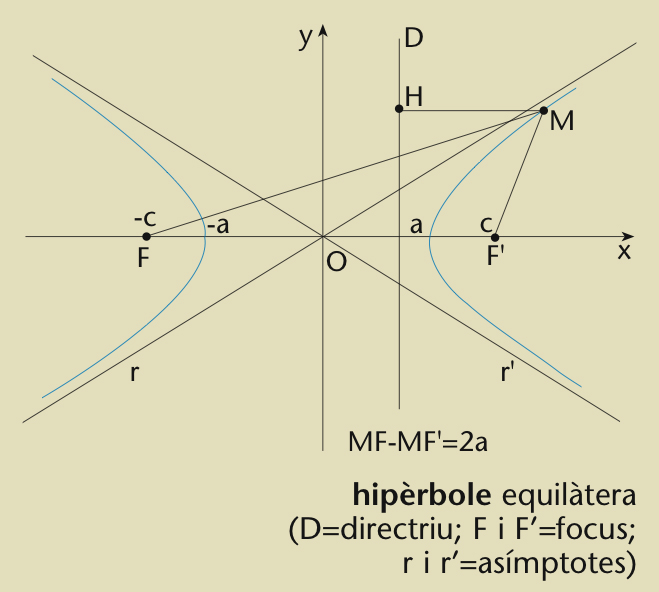
Hipèrbole equilàtera
© Fototeca.cat
Matemàtiques
Corba oberta, intersecció d’un con de revolució amb un pla que forma amb ’eix d’aquell un angle més petit que amb la generatriu.
Constitueix el lloc geomètric dels punts del pla tals que la diferència de llurs distàncies a dos punts fixos, anomenats focus , és una constant, simbolitzada habitualment per 2 a Té dos eixos de simetria i, referida a ells, la seva equació és x 2 / a 2 - y 2 / b 2 = 1, on i 2c és la distància entre els focus L’excentricitat e és c / a Les asímptotes són les rectes y = b / a x asímptota Quan a = b , la hipèrbola és anomenada equilàtera , i la seva equació referida a les asímptotes, que són perpendiculars, és y = k/ x la seva excentricitat és
enter
Matemàtiques
Classe d’equivalència que la relació (a,b)R(c,d), si, i només si, a+d = b+c, indueix en el conjunt producte ℕ × ℕ (ℕ essent el conjunt dels nombres naturals).
El conjunt d’aquestes classes d’equivalència conjunt quocient és el conjunt dels nombres enters ℤ = {0, ±1, ±2, ±3, } Hom anomena representant canònic d’un enter a,b aquell en què o a o b és 0 Si l’esmentat representant canònic és de la forma m, 0, aquest és un enter positiu , representat també per + m si és la forma 0, m , es tracta d’un enter negatiu , habitualment representat per - m i si és 0,0, és l' enter nul , o sigui 0 En el conjunt ℤ hom defineix dues operacions la suma és definida per a, b + c, d = a + c , b + d , i el producte , per a, b c, d = ac + bd…
criptografia
Matemàtiques
Aplicació de tècniques matemàtiques que permeten xifrar i desxifrar missatges, de manera que només pugui ésser interpretat pel receptor al qual van adreçats.
Hi ha diferents estratègies per a xifrar la informació, però gairebé totes consisteixen a modificar algun paràmetre de la comunicació segons una seqüència pseudoaleatòria coneguda per l’emissor i pel receptor La seqüència és pseudoaleatòria en aquest sentit el receptor que desconeix la clau amb què ha estat generada interpreta que és del tot aleatòria, mentre que aquell que sí que la coneix pot reproduir la seqüència amb una certa facilitat El xifratge de la informació s’estén a tot tipus de comunicació que requereixi un cert grau de seguretat i als sistemes de radiodifusió de pagament La…
càlcul de diferències
Matemàtiques
Estudi de les propietats d’una funció de la qual hom només coneix un conjunt finit de valors f(x0), f(x1), ..., f(xn), que corresponen als arguments x0, x1, ..., xn, els quals, habitualment, són presos en progressió aritmètica xr=x0+rϖ.
Hom defineix l’ operador diferència Δ, mitjançant l’expressió Δf x = f x + ϖ - f x , i l’ operador incremental E , definit per E ϖ f x = f x + ϖ = f x + Δ f x , de manera que E = 1+Δ Les propietats d’aquests permeten d’assolir el resultat següent, dit teorema de Gregory f x + nϖ = E nϖ f x = 1+Δ n f x , on, en l’última expressió, hom pot emprar la fórmula del binomi de Newton Aquests operadors poden expressar les diferències dividides Hom pot obtenir una aproximació polinòmica a la funció f x amb la fórmula d’interpolació de Newton en la qual, si f x és n vegades…
trigonometria

1, circumferència de referència per a la definició de les raons trigonomètriques; 2, representació gràfica de les línies trigonomètriques; 3, símbols emprats en la resuloció de triangles
© fototeca.cat
Matemàtiques
Part de la matemàtica inicialment dedicada a l’estudi de les relacions entre les amplituds dels angles i les longituds dels segments que llurs costats determinen en les rectes que tallen.
La trigonometria es basa en les propietats de les anomenades raons trigonomètriques , que són definides a partir d’un punt P x,y d’una circumferència de centre O i per l’angle α que forma el radi r = OP amb l’eix OX , mitjançant els sis quocients següents sin α = y/r sinus cos α = x/r cosinus tg α = y/x tangent cotg α x/y cotangent sec α = r/x secant cosec α = r/y cosecant Quan el punt P és a una distància r = 1 de l’origen O , el valor absolut d’aquestes raons és representat per la longitud de certs segments anomenats línies trigonomètriques , respectivament, fàcils de traçar A partir de…