Resultats de la cerca
Es mostren 61 resultats
aïllat | aïllada
Matemàtiques
Dit del sistema d’equacions en què s’han trobat els valors de certes incògnites.
sistema d’equacions
Matemàtiques
Conjunt d’equacions que han d’ésser satisfetes per un mateix conjunt de valors de les variables.
Si les equacions del sistema són totes de primer grau sistemes lineals la discussió i la resolució són obtingudes pel teorema de Rouché-Frobenius i la regla de Cramer
dada
Matemàtiques
En una investigació matemàtica, cadascun dels elements coneguts (magnituds, figures, relacions) a partir dels quals han d’ésser deduïts els elements desconeguts.
teoria
Matemàtiques
Conjunt de principis referents a un determinat concepte (o conceptes) que inclou tant els axiomes postulats sobre aquest com les conseqüències (teoremes) que d’aquests axiomes han estat deduïdes lògicament.
Així, la teoria de funcions estudia les funcions reals o les complexes funció la teoria d’equacions estudia els mètodes de resoldre equacions, les relacions entre les solucions i les que hi ha entre aquestes i els coeficients de les equacions equació Cal esmentar també altres teories d’una gran importància, com la teoria de grups grup, la de conjunts conjunt, la de nombres nombre, la dels jocs , la de probabilitats probabilitat, la de catàstrofes catàstrofe, la de sistemes sistema, etc
Nicolas Bourbaki
Matemàtiques
Pseudònim col·lectiu d’un grup de matemàtics francesos, antics alumnes de l’École Normale Supérieure.
El 1930 començà a aparèixer aquesta signatura en els Comptes Rendus de l’Académie Française des Sciences, i a partir del 1939 iniciaren la publicació dels cèlebres Éléments de Mathématiques Adscrits a l’escola formalista formalisme , han exercit una gran influència en la matemàtica actual l’elaboració dels Éléments sembla ésser una realització del programa de David Hilbert Bé que el funcionament intern i el nom dels membres del grup Bourbaki han estat mantinguts en secret, hom creu que els fundadors foren Henri Cartan, Claude Chevalley, Samuel Eilenberg, Jean…
flexàedre
Matemàtiques
Políedre flexible de cares rígides.
Els flexàedres han de tenir necessàriament més de set vèrtexs, i hom n’ha construït de nou vèrtexs i de més
arbre
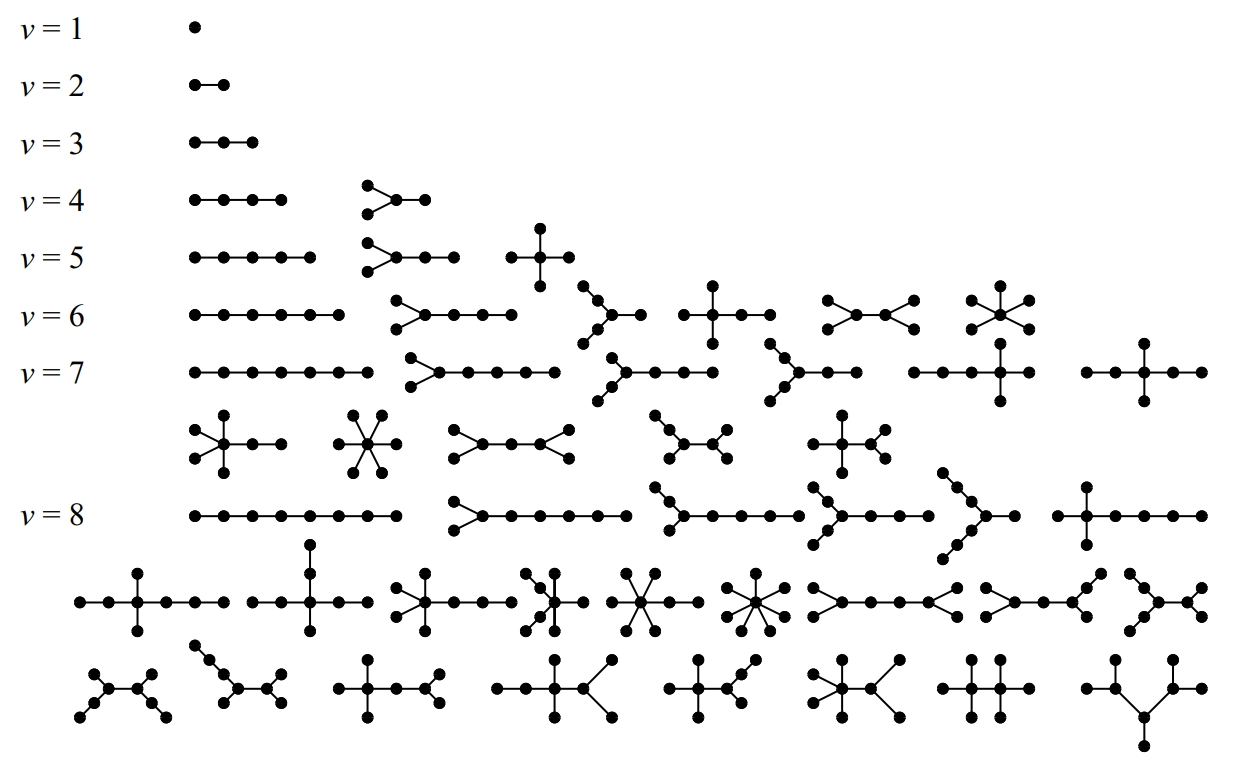
Tots els arbres amb vuit vèrtexs com a màxim
© fototeca.cat
Matemàtiques
Graf connex i acíclic (sense circuits).
Un arbre té només un vèrtex, anomenat arrel sense predecessor en el sentit de les fletxes, mentre que tot altre vèrtex té, cada un, un únic predecessor Tots els vèrtexs tenen un nombre variable de successors, que ordinariàment hom suposa ordenats per exemple, d’esquerra a dreta i de vegades són anomenats branques En la representació habitual d’un arbre l’arrel se situa al capdamunt i els arcs se suposen recorreguts en sentit descendent Els arbres han passat d’ésser un cas particular de graf a rebre un tractament matemàtic específic Són particularment útils en la modelització de processos en…
Ivan Stephan Sokolnikov
Matemàtiques
Matemàtic ucraïnès, naturalitzat nord-americà.
Estudià els mètodes per a resolució dels problemes de la teoria matemàtica de l’elasticitat i la mecànica dels medis continus Ha publicat nombrosos llibres i articles que l’han fet mundialment conegut i famós
Jerzy Neyman
Matemàtiques
Matemàtic soviètic, naturalitzat nord-americà.
Juntament amb ESPearson estudià la teoria dels tests d’hipòtesis estadístiques, en la qual introduïren el concepte de potència d’un test i els de primer i segon risc d’error Els seus mètodes estadístics han estat aplicats amb èxit a qüestions concretes d’astrofísica i de cibernètica
Andrew John Wiles
Matemàtiques
Matemàtic anglès.
Format a Anglaterra, resideix, però, als EUA Ha fet importants treballs algebraics que li han permès demostrar finalment la certesa de la conjectura de Fermat ‘no hi ha nombres enters x,y,z que satisfacin la relació x n + y n = z n , quan n és major o igual a 3’
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- Pàgina següent
- Última pàgina