Resultats de la cerca
Es mostren 4 resultats
Frigyes Riesz
Matemàtiques
Matemàtic hongarès.
Estudià les equacions integrals, les funcions harmòniques i la teoria ergòdica i establí la teoria dels operadors compactes És considerat com un dels creadors de l’anàlisi funcional moderna
Georges-William de Rham
Matemàtiques
Matemàtic suís.
Es graduà a Lausana 1925 Doctorat a París 1931, fou professor de les universitats de Lausana 1932, París 1943 i Ginebra 1953-73 S'especialitzà en qüestions de geometria diferencial de topologia, on obrí nous camins de recerca i formulà uns teoremes que duen el seu nom És autor de Variétés différentiables Formes courants, formes harmoniques 1955 En 1963-66 fou president de la Unió Matemàtica Internacional
equació de Laplace
Física
Matemàtiques
Equació diferencial en derivades parcials expressada per la fórmula Δf = 0, Δ essent el laplacià.
Les funcions que són solució de l’equació de Laplace són anomenades funcions harmòniques , i tenen una especial aplicació en la teoria del potencial En el cas que f sigui una funció de la variable complexa z = x + iy , l’equació de Laplace, que en aquest cas pren la forma ∂ 2 f /∂ x 2 + ∂ 2 f /∂ y 2 = 0, expressa la condició necessària i suficient perquè f sigui derivable
número d’or
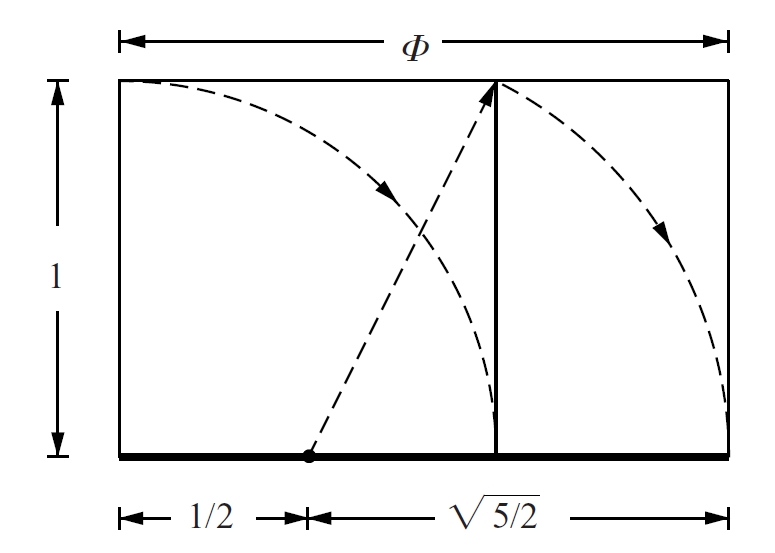
número d’or
Matemàtiques
Nombre irracional algebraic positiu que, elevat al quadrat, és igual a ell mateix més una unitat: (1 + ⎷5 ) ⁄ 2 = 1,618.
El número d’or apareix en molts problemes geomètrics relatius a les divisions harmòniques de segments o a proporcions de rectangles, o entre mides Així, un rectangle té de proporció el número d’or si, i solament si, té la mateixa proporció del rectangle que resulta de treure del rectangle original un quadrat Aquest nombre és el límit dels quocients 1 ⁄ 1, 2 ⁄ 1, 3 ⁄ 2, 5 ⁄ 3 dels termes de la successió de Fibonacci i té una important presència en elements naturals i artístics, especialment en pintura i arquitectura, ja que que el número d’or és igual al cosinus de 36º i, per tant, està lligat…