Resultats de la cerca
Es mostren 478 resultats
corba de Peano
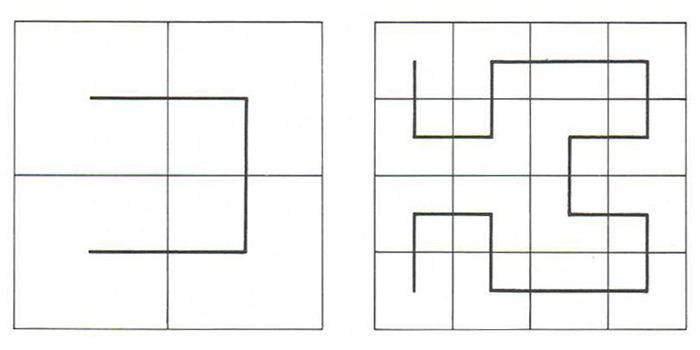
Corba de Peano traçada unint els punts centrals dels successius quadrats en què hom divideix el quadrat inicial
© fototeca.cat
Matemàtiques
Donat un quadrat, corba que, amb una longitud finita des del seu començament, ateny qualsevol punt del quadrat inicialment fixat.
nombre real
Matemàtiques
Cadascun dels nombres que hom pot obtenir en mesurar magnituds contínues.
Hom obté el conjunt dels nombres reals completant el conjunt dels nombres racionals amb tots els nombres irracionals que poden ésser representats sobre la recta, tals com etc La manera més simple d’introduir teòricament i d’utilitzar en la pràctica els nombres reals és per mitjà de llur expressió decimal Tot nombre real és expressat en forma decimal amb infinites xifres que, en el cas dels nombres irracionals, no es repeteixen periòdicament Això suposa que per a definir un nombre real cal donar una llei que permeti d’obtenir tantes xifres decimals com hom vulgui A la…
infinit
Matemàtiques
Dit del valor més gran que qualsevol altre que hom pugui donar.
Es representat amb el símbol ∞ Així, hom diu que una variable x tendeix a infinit x →∞ o que una funció f x tendeix a inifinit per a
límit d’una successió
Matemàtiques
Valor al qual una successió s’acosta més i més (tant com hom vulgui).
Donada una successió { a n }, a 1 ,, a n ,, hom diu que el límit de la successió és A , o que la successió tendeix a a , si per a tot real ε > 0, per petit que sigui, existeix un terme a m de la successió tal que si n > m aleshores | A-a n |
combinació
Matemàtiques
Configuració on hom només té en compte la distinció entre els elements agrupats i no l’ordre en què són presos.
Hom anomena combinació d’ordre n , formada a partir d’un conjunt de m elements 0 ≤ n≤ m, qualsevol dels subconjunts formats en considerar n elements diferents entre els m que integren el conjunt donat, sense tenir-ne en compte l’ordre hom considera, doncs, que dues combinacions són distintes quan algun de llurs elements és diferent El nombre de combinacions d’ordre n , formades a partir d’un conjunt amb m elements, és donat per l’expressió on V n m indica el nombre de variacions, i P n el de permutacions Hom representa sovint C n m per n m , parlant, en…
fiabilitat
Matemàtiques
Tecnologia
Mesura de la confiança que hom pot tenir en el funcionament correcte d’un sistema o d’un dels elements que el componen.
Hom l’expressa per la probabilitat que s’acompleixi aquest funcionament correcte durant un temps determinat i en condicions especificades de funcionament La fiabilitat variarà amb aquestes condicions, tant si són pròpies del sistema com si són externes Hom pot estudiar la fiabilitat d’un element i la del sistema en el seu conjunt en funció del temps mitjançant tres nocions interrelacionades la supervivència, la duració de vida i la probabilitat condicional de falliment o d’avaria, la més instructiva de les quals és la tercera amb un nombre suficient d’observacions…
factorial
Matemàtiques
Producte dels nombres naturals consecutius, des de l’1 fins al nombre del qual hom calcula el factorial.
És indicat per n La generalització de la noció de factorial a nombres no naturals és possible mitjançant la funció Γ d’Euler gamma Per a molt gran, hom pot calcular n aproximadament per mitjà de la fórmula de Stirling
logaritme augmentat
Matemàtiques
Logaritme decimal d’un nombre menor que 1, a la característica del qual, que és negativa, hom ha aplicat cert artifici per tal que sigui sempre positiva.
L’artifici consisteix a sumar a la característica el nombre de desenes positives que calgui per tal que sigui positiva, tot posant aquest nombre de desenes com a superíndex de la característica superíndex que hom anomena augment Així, hom substitueix la característica negativa a per 10 n - a n , n essent un nombre enter positiu tal que 10 n > ¦ a ¦ Els logaritmes augmentats foren ideats per tal de disminuir les probabilitats d’error en les operacions amb logaritmes en certs tipus de càlculs, com en els de navegació astronòmica, artilleria, topografia, etc
funció gamma
Matemàtiques
Funció definida per la fórmula, deguda a Euler, Γ( x
) = ∫
t ( x - 1 )
e - t
, on, si hom considera Γ real, x
ha d’ésser real i major que zero, i si hom considera Γ complexa, la part real de x
ha d’ésser major que zer¦.
Segons Gauss, hom pot definir també la funció Γ amb l’expressió on x pot ésser qualsevol nombre real o complex, excepte enter negatiu Les propietats immediates de la funció Γ són Γ x +1 = x Γ x Γ1 = 1 Γ n = n-1 , per a n natural Una aplicació important de la funció Γ és que permet de generalitzar el concepte de factorial a nombres reals no enters i a nombres complexos
fase
Física
Matemàtiques
Argument de les funcions sinusoïdals (sinus o cosinus), dependents del temps, especialment quan hom les considera en les formes u = U sin (ϖt+ϕ) i u = U cos (ϖt+ϕ).
És emprat per a descriure l’elongació d’un moviment harmònic o el valor d’una magnitud variable en corrent altern Dues magnituds u 1 i u 2 , variables periòdicament amb el mateix període, són en fase quan en tot instant tenen ambdues la mateixa fase altrament presenten una diferència de fase o desfasament , i hom diu que són desfasades Quan són desfasades π radiants hom diu que són en oposició , i quan ho són π/2 radiants, en quadratura El valor de la fase a l’instant t = 0 és anomenat fase inicial
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina