Resultats de la cerca
Es mostren 10 resultats
funció zeta
Matemàtiques
Funció complexa, introduïda per Riemann.
Definida per la fórmula on z = x + iy ∈ℂés tal, que x > 1 i ln n és real És una funció meromorfa amb un pol simple en z = 1
regla de falsa posició
Matemàtiques
Mètode per a resoldre l’equació a x = b, utilitzat abans d’ésser inventada la notació algèbrica actual, consistent a utilizar la fórmula (escrita en la notació actual) on x1 i x2 són nombres tals que .
La regla, doncs, era aplicada determinant dos nombres x 1 , x 2 tals que a x 1 i a x 2 superessin b i determinant a continuació les diferències d 1 i d 2 abans de determinar x Aquesta regla, que fou introduïda a Europa pels àrabs, probablement procedia de la Xina
Berthold Schweizer
Matemàtiques
Matemàtic alemany, naturalitzat nord-americà des del 1937.
Deixeble del prestigiós matemàtic Karl Menger, fou professor a les universitats de Califòrnia, Arizona i Massachusetts Amherst Impartí cursos en diverses universitats europees i publicà un gran nombre de treballs de recerca Especialista en àlgebra de funcions i en equacions funcionals, conjuntament amb Abe Sklas, fou fundador de la teoria dels espais mètrics probabilístics idea introduïda per Menger, disciplina d’un extraordinari interès científic
matroide
Matemàtiques
Estructura algèbrica consistent en un conjunt E i un conjunt S de parts no buides de E que satisfan: tot singletó de E pertany a S
.
Si X ∈S , aleshores tota part Y no buida de E inclosa en X pertany també a S i, per a tota part A de E , si X i Y són dos elements de S continguts en A i maximals, aleshores card X = card Y La teoria de matroides fou introduïda per Withney el 1935 i ha experimentat un desenvolupament ràpid en ésser aplicada als espais vectorials i a la teoria de grafs
nombre complex
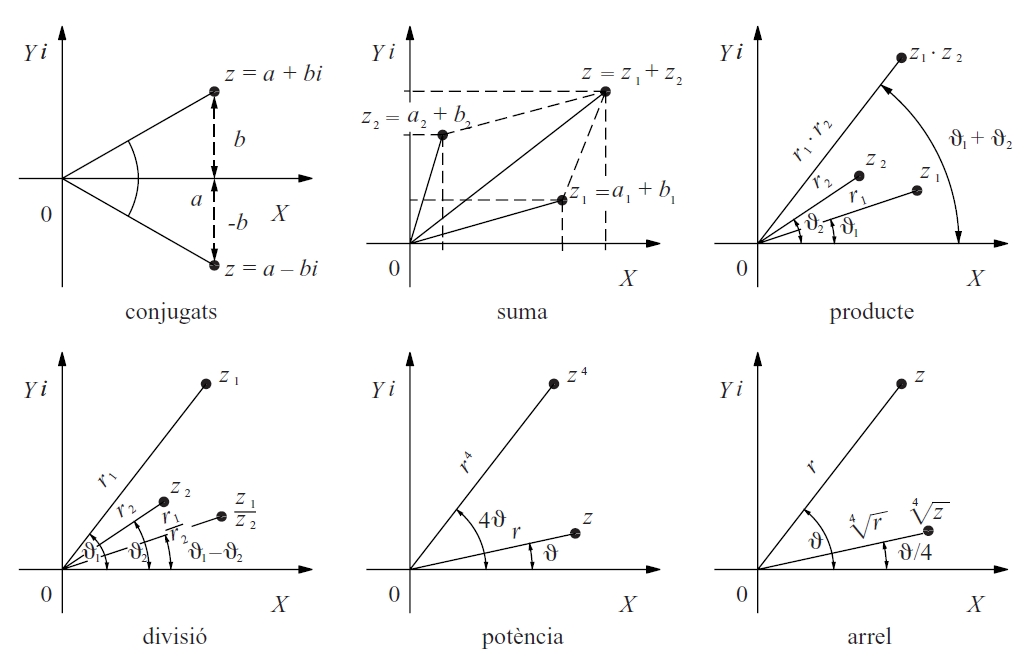
Nombres complexos
Matemàtiques
Nombre que pot ésser expressat com a suma d’un nombre real i d’un nombre imaginari.
Hom construeix el conjunt ℂ dels nombres complexos afegint al conjunt dels nombres reals un nombre nou, no real, que hom representa per una i , i que és definit formalment per la propietat que el seu quadrat és -1 Hom estén a aquest conjunt ℂ les operacions d’addició i de multiplicació amb totes les propietats que tenen entre nombres reals Cada nombre complex pot ésser escrit en forma de polinomi de primer grau en i , a + bi , i pot ésser representat geomètricament en el pla prenent a i b com a coordenades en un sistema cartesià ortogonal pla d'Argand-Gauss Aquesta…
càlcul de variacions
Matemàtiques
Estudi de la teoria dels extrems d’integrals definides tals, que llur integrant és una funció coneguda d’una o més variables independents, d’una o més variables dependents i de les seves derivades.
El problema consisteix a determinar les variables dependents, de manera que la integral sigui màxima o mínima En el cas més simple, la integral és de la forma on cal determinar la funció y x de manera que I sigui màxima o mínima També poden ésser considerades integrals de la forma on y 1 , , y n són funcions de x desconegudes o bé integrals múltiples tals com on z = z x,y és desconeguda com també poden ser-ho com integrals múltiples d’ordre superior o de diverses variables dependents L’integrant pot ésser també una funció en la qual intervinguin derivades parcials d’ordre superior En el…
llei de Student
Matemàtiques
Llei, coneguda també com a llei t de Student, introduïda per W. S. Gossett, que correspon a la funció de distribució següent: .
El paràmetre n és anomenat graus de llibertat de la llei Quan n tendeix a infinit, aquesta distribució tendeix a una distribució normal , però, de fet, per a n major de 30 la llei normal ja és una bona aproximació Això fa que aquesta llei sigui emprada com a prova d’hipòtesi per a analitzar si una distribució és normal o no
godelització
Matemàtiques
Tècnica introduïda per Kurt Gödel l’any 1931 que consisteix a reduir a nombres naturals les paraules i frases d’un cert llenguatge.
Si hom disposa d’un cert llenguatge L = { a 1 ,, a n } i a cada símbol a i li associa un cert nombre senar g a i per exemple, g a i = 2 i + 1 i, a cada paraula , on cada és una de les lletres a j ∈ L , el nombre , on p r és el r -èsim nombre primer Ara hom pot estendre aquesta tècnica a frases, on cada OOO és una de les lletres
teoria de categories
Matemàtiques
Teoria introduïda cap al 1940 pels matemàtics S. Eilenberg i S. MacLane, fonamentada sobre el concepte de categoria, i aplicada inicialment en la topologia algèbrica.
És utilitzada en tot aquell tipus de problema algèbric on hom té una estructura de base i un conjunt de propietats genèriques que no depenen de la realització en un objecte matemàtic concret, especialment en àlgebra homològica i geometria algèbrica
relació de proximitat
Matemàtiques
Relació binària S entre els subconjunts d’un conjunt E, que fou introduïda per Efremovič per tal de generalitzar la relació ‘‘ésser pròxim’’ que hom utilitza correntment en l’espai mètric ordinari.
La relació de proximitat és definida pels axiomes següents ASB ⇔ BSA , és a dir, la relació S és simètrica ASB ⇒ A ≠∅i B ≠∅, és a dir, el conjunt buit no és pròxim a cap altre AS B ∪C ⇒ ASB o ASC , és a dir, un conjunt és pròxim a la reunió de dos conjunts si és pròxim, almenys, a un d’ells A ∩B ≠∅⇒ASB , és a dir, dos conjunts que es tallen són pròxims { X } S { Y } ⇔ X=Y , és a dir, un punt només és pròxim a si mateix si A$B aleshores existeix un conjunt C tal que B$C i A$C c , on C c és el conjunt complementari de C Tota proximitat indueix una topologia prenent com a conjunts tancats els…