Resultats de la cerca
Es mostren 15 resultats
funció algèbrica
Matemàtiques
Funció que pot ésser expressada usant només les operacions addició, subtracció, multiplicació, divisió i elevació a una potència racional.
Les funcions polinòmiques, racionals i irracionals són algèbriques
Hugues Charles Robert Méray
Matemàtiques
Matemàtic francès.
Contribuí a les teories modernes sobre el sistema dels nombres reals i fou un dels primers a establir-ne el continu Definí aritmèticament els nombres irracionals sense referir-se als límits Escriví Exposition nouvelle de la théorie des formes linéaires 1884 i Nouveaux éléments de géometrie 1903
Julius Wilhelm Richard Dedekind

Julius Wihelm Richard Dedekind
© Fototeca.cat
Matemàtiques
Matemàtic alemany, deixeble de Gauss.
Professor al politècnic de Zuric 1858 i a la Technische Hochschule de Brunsvic 1862-1912, ha estat un dels capdavanters de dos dels corrents bàsics que han donat origen i suport a la matemàtica moderna el formalista culminat en l’obra de Hilbert, que bandeja qualsevol possibilitat d’incloure un raonament basat en la intuïció dins l’edifici matemàtic, i el logicista Was sind und was sollen die Zahlen , ‘Què són i per a què serveixen els nombres', 1888, que pretén de situar la matemàtica com a branca particular de la lògica, elaborat fins a les darreres conseqüències per Russell Construí una…
nombre real
Matemàtiques
Cadascun dels nombres que hom pot obtenir en mesurar magnituds contínues.
Hom obté el conjunt dels nombres reals completant el conjunt dels nombres racionals amb tots els nombres irracionals que poden ésser representats sobre la recta, tals com etc La manera més simple d’introduir teòricament i d’utilitzar en la pràctica els nombres reals és per mitjà de llur expressió decimal Tot nombre real és expressat en forma decimal amb infinites xifres que, en el cas dels nombres irracionals, no es repeteixen periòdicament Això suposa que per a definir un nombre real cal donar una llei que permeti d’obtenir tantes xifres decimals com hom vulgui A la…
binomi de Newton
Matemàtiques
Fórmula per a calcular la potència enèsima d’un binomi, anomenada també teorema del binomi.
En el cas que l’exponent n del binomi sigui un nombre natural, la fórmula pot ésser demostrada per inducció, i la seva expressió és on els coeficients n k , anomenats coeficients binomials , són donats per la fórmula Aquesta expressió, que ja utilitzà NTartaglia, fou ampliada per INewton en el cas d’exponents negatius i fraccionaris i per LEuler en el cas d’exponents irracionals En el cas, però, que l’exponent n no sigui un nombre natural, l’anterior expressió esdevé una sèrie infinita i, per tant, només té sentit quan la sèrie és convergent, cosa que imposa certes limitacions…
fracció contínua
Matemàtiques
Expressió de la forma
on l’algorisme s’estén indefinidament.
Hom l’expressa abreujadament mitjançant la notació a 0 + a 1 / b 1 + a 2 / b 2 + a 3 / b 3 + Són emprades per a representar nombres irracionals Així, si α 0 és un nombre irracional positiu, i n ≥0, α 0 admet l’expressió on u n és la part entera de α i α n ≥1 és definit per la relació de recurrència α n - 1 = u n - 1 + 1/α n , n≥1 La successió u n n ≥ 0 és el desenvolupament de α 0 en fracció contínua , i els coeficients u n són els quocients incomplets de la fracció contínua Un exemple d’aquest tipus de desenvolupament és el del nombre π/4, fet per William Brouncker
teorema de Pitàgores
Matemàtiques
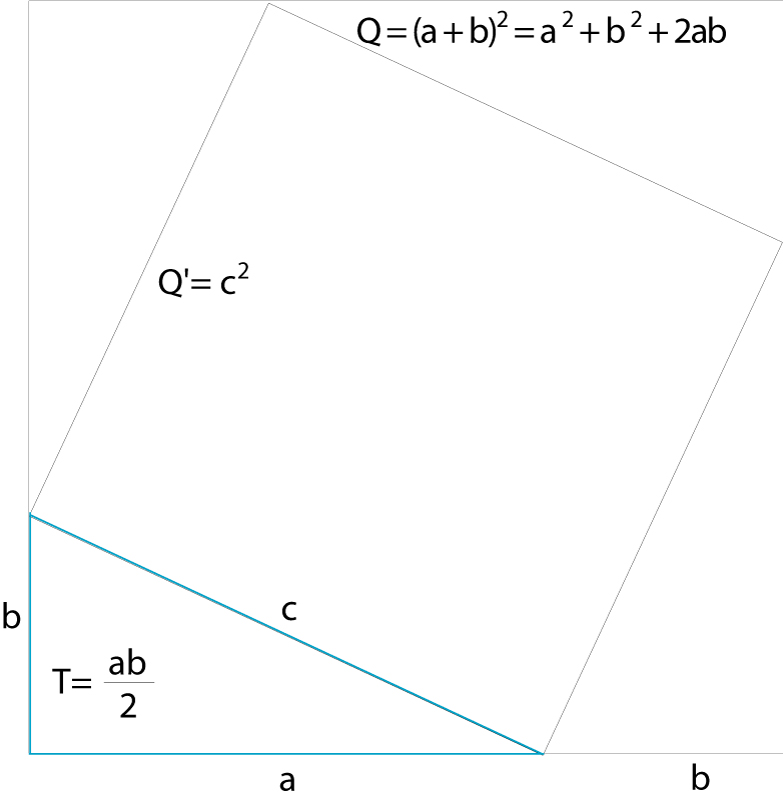
Teorema fonamental de la geometria segons el qual en un triangle rectangle l’àrea del quadrat que té per costat la hipotenusa és igual a la suma de les àrees dels quadrats que tenen per costat els catets.
Si a i b representen les longituds dels catets i c la longitud de la hipotenusa, el teorema Pitàgores és expressat per la igualtat c 2 = a 2 + b 2 Bé que la primera demostració del teorema sembla que fou feta pels membres de l’ escola pitagòrica Pitàgores vers l’any 550 aC, el teorema de Pitàgores, almenys en alguns casos particulars, ja era conegut pel poble egipci vers l’any 2000 aC, pels xinesos vers l’any 1100 aC i pels vedes vers l’any 800 aC D’altra banda, fou a partir del teorema que els pitagòrics descobriren que no n'hi ha prou amb els nombres enters i fraccionaris per a mesurar…
Georg Cantor

Georg Cantor
© Fototeca.cat
Matemàtiques
Matemàtic alemany.
Estudià a Zuric, Göttingen i Frankfurt, i es doctorà en filosofia a Berlín 1867 Fou professor a la Universitat de Halle Wittenberg des del 1872 al 1905 La seva obra abastà els camps de l’anàlisi, la topologia i la lògica matemàtica Creador de la teoria de conjunts, la seva anàlisi del concepte d’infinit ha plantejat la necessitat d’un examen crític dels mateixos fonaments de les matemàtiques Definí el concepte de cardinal per a conjunts finits i infinits Així mateix, desenvolupà la teoria dels nombres irracionals, introduí els nombres transfinits i definí, alhora que Julius…
nombre
Matemàtiques
Resultat de comptar les coses que formen un agregat (dos, tres, quatre, etc., i també un, o sia, la unitat) o qualsevol dels ens abstractes que resulten de generalitzar aquest concepte.
El concepte de nombre ha anat evolucionant al llarg de la història així, al principi anava enllaçat amb el simple ús de xifres o guarismes per a comptar sistemes de numeració Els nombres 1, 2, 3, 4, etc, ja eren usats en les antigues cultures babilònica, egípcia, xinesa la qual coneixia els negatius i índia la qual introduí el zero Aquest ús de xifres no implicava, però, cap concepte abstracte de nombre A l’antiga Grècia els pitagòrics consideraren que el nombre era una estructura determinada, immanent a totes les coses això generà la numerologia grega o mística, basada en les propietats…
nombre racional
Matemàtiques
Conjunt de fraccions equivalents que representen una mateixa quantitat, entera o no.
Dues fraccions a / b , c / d són equivalents o iguals si, i només si, els parells de nombres enters que les constitueixen compleixen la relació ad = bc Cada classe de fraccions equivalents en aquesta relació d’equivalència és un nombre racional Si la fracció que defineix un nombre racional té numerador múltiple del denominador, és a dir, a = kb k ∈ℤ, la fracció a / b és equivalent a k/ 1, que hom acostuma a escriure en la forma k/ 1 = k En aquest sentit hom pot dir que els nombres enters són un subconjunt dels racionals Entre els nombres racionals hom pot definir les operacions d’addició i…