Resultats de la cerca
Es mostren 12 resultats
Reial Acadèmia de Ciències i Arts de Barcelona

Emblema de la Reial Acadèmia de Ciències i Arts de Barcelona
© Fototeca.cat
Entitats culturals i cíviques
Matemàtiques
Astronomia
Física
Química
Geologia
Biologia
Tecnologia
Institució fundada l’any 1764 amb el nom de Conferència Fisicomatemàtica Experimental amb Francesc Subiràs com a president i Josep Anton Desvalls, marquès de Llupià, com a secretari, limitada inicialment a 16 membres.
Celebrà les primeres reunions a la rebotiga d’una farmàcia i més tard a unes golfes del carrer de la Boqueria, on fou installat un gabinet de màquines d’experimentació El desembre del 1765 es reorganitzà amb el nom de Reial Conferència Física , amb uns nous estatuts pels quals fou designat president el capità general de Catalunya, i amplià el seu abast al conreu de “totes les ciències naturals i l’avenç de les arts útils”, amb nou seccions àlgebra i geometria estàtica i hidroestàtica electricitat magnetisme i òptica pneumàtica i acústica història natural botànica química agricultura El 1770…
Nicolas Bourbaki
Matemàtiques
Pseudònim col·lectiu d’un grup de matemàtics francesos, antics alumnes de l’École Normale Supérieure.
El 1930 començà a aparèixer aquesta signatura en els Comptes Rendus de l’Académie Française des Sciences, i a partir del 1939 iniciaren la publicació dels cèlebres Éléments de Mathématiques Adscrits a l’escola formalista formalisme , han exercit una gran influència en la matemàtica actual l’elaboració dels Éléments sembla ésser una realització del programa de David Hilbert Bé que el funcionament intern i el nom dels membres del grup Bourbaki han estat mantinguts en secret, hom creu que els fundadors foren Henri Cartan, Claude Chevalley, Samuel Eilenberg, Jean Dieudonné i André…
algorisme d’Euclides
Lògica
Matemàtiques
Successió de divisions enteres que condueixen a la determinació del màxim comú divisor
(mcd) de dos nombres enters.
Així, el mcd dels nombres a i b s’obté fent ab que dóna resta r, br que dóna resta r 1 , rr 1 que dóna resta r 2 , etc La darrera resta no nulla és el mcd dels membres a i b
desigualtat de Bernoulli
Matemàtiques
Si dos membres reals, x i a, satisfan x>-1 i a>1, aleshores (1+x)a> 1+ax.
Real Academia de Ciencias Exactas, Físicas y Naturales
Matemàtiques
Institució científica resident a Madrid que té per objecte promoure l’estudi i el progrés de les ciències.
Té el seu origen en l’Academia Naturae Curiosorum 1657 de Madrid, que fou substituïda el 1834 per l' Academia de Ciencias Naturales El seu nom actual data del 1847, i els seus estatuts, del 1921 Consta de 37 membres numeraris, de 42 corresponents i de 78 d’estrangers A més de les Memorias i dels Anales , publica la Revista de los progresos de las ciencias
Nomenclatura d’Unitats Territorials Estadístiques
Matemàtiques
Sistema de denominacions elaborat per l’EUROSTAT per a la Comunitat Europea (1972).
A partir de les unitats administratives o funcionals dels estats membres, el sistema normalitza tres nivells I, regions comunitàries europees II, unitats administratives de base i III, subdivisions de les unitats II Permet, a més, la integració per agrupacions successives sempre passant pels estats, l’homogeneïtzació estadística i les modificacions per ésser un sistema obert, i possibilita de conèixer l’evolució territorial, tot establint la política regional més adient
Andrej Andrejevič Markov
Matemàtiques
Matemàtic rus, deixeble de P.L. Čebyšev.
Fou un dels membres més destacats de l’escola de matemàtics russos dedicats a l’estudi de la teoria de probabilitats Treballà especialment en la llei dels grans nombres, i analitzà els processos estocàstics, els quals considerà com una cadena de proves, que ha estat anomenada cadena de Markov Aplicà els seus coneixements matemàtics a la lingüística anàlisi de Markov per a estudiar la freqüència dels mots i de llurs encadenaments
teorema de Pitàgores
Matemàtiques
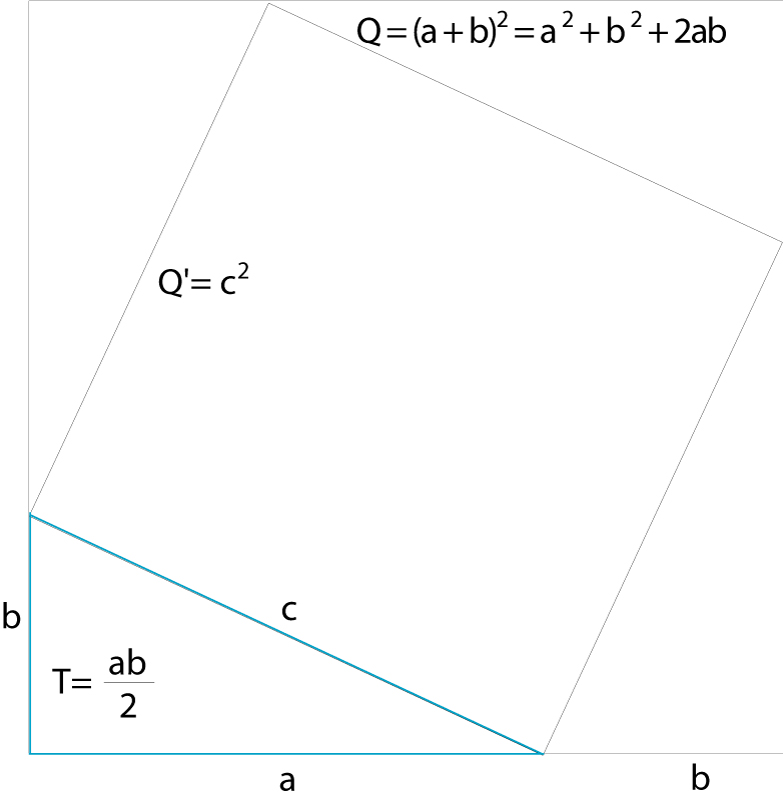
Teorema fonamental de la geometria segons el qual en un triangle rectangle l’àrea del quadrat que té per costat la hipotenusa és igual a la suma de les àrees dels quadrats que tenen per costat els catets.
Si a i b representen les longituds dels catets i c la longitud de la hipotenusa, el teorema Pitàgores és expressat per la igualtat c 2 = a 2 + b 2 Bé que la primera demostració del teorema sembla que fou feta pels membres de l’ escola pitagòrica Pitàgores vers l’any 550 aC, el teorema de Pitàgores, almenys en alguns casos particulars, ja era conegut pel poble egipci vers l’any 2000 aC, pels xinesos vers l’any 1100 aC i pels vedes vers l’any 800 aC D’altra banda, fou a partir del teorema que els pitagòrics descobriren que no n'hi ha prou amb els nombres enters i fraccionaris…
base d’un espai topològic
Matemàtiques
Família de conjunts oberts d’un espai topològic tal que qualsevol conjunt obert de la topologia és la unió d’alguns membres de la família.