Resultats de la cerca
Es mostren 8 resultats
obert | oberta
Matemàtiques
En un espai mètric E, dit del conjunt C tal, que donat un punt qualsevol a de C existeix una distància d tal, que tots els punts de E situats a una distància del punt a inferior a d pertanyen al conjunt C.
Així, entre els intervals de la recta real, els únics oberts són els intervals oberts interval Les propietats formals dels conjunts oberts han conduït a la formulació de l’anomenada topologia general , en la qual la noció d’obert és una noció primitiva que només és subjecta als tres axiomes següents el conjunt buit és obert, tota unió de conjunts oberts és un conjunt obert, i tota intersecció finita de conjunts oberts és un conjunt obert
bola
Matemàtiques
En un espai mètric amb una distància d, conjunt de punts x la distància dels quals a un cert punt fix a és menor (o igual) que un nombre fix r (r > 0); es parla, aleshores, de la bola oberta (tancada) de radi r i de centre a.
Usualment es denota per B a r la bola oberta i per B̄ a r la bola tancada A ℝ les boles obertes són els intervals oberts i les boles tancades són els intervals tancats
paràbola
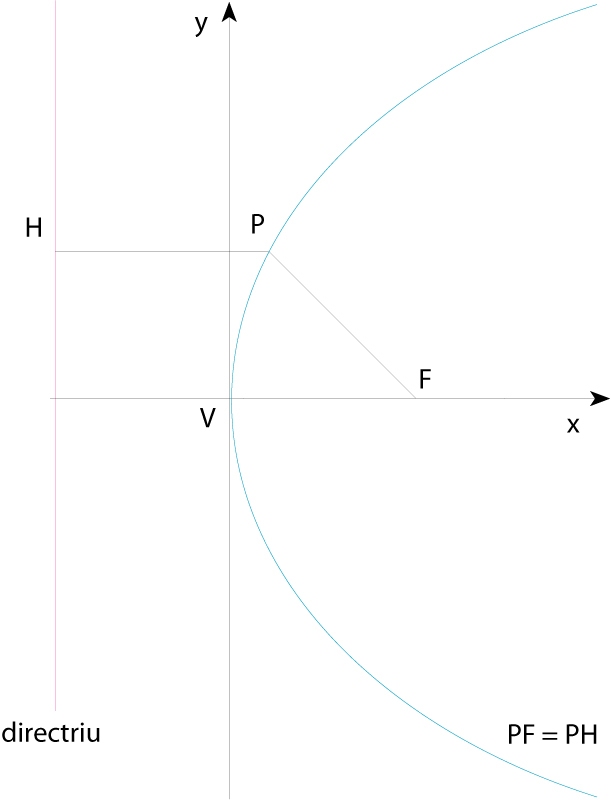
Paràbola (V vèrtex, F focus, P punt qualsevol de la paràbola)
© Fototeca.cat
Matemàtiques
Corba oberta, intersecció d’una superfície cònica amb un pla paral·lel a una de les generatrius.
Constitueix el lloc geomètric dels punts del pla que equidisten d’un punt el focus de la paràbola i d’una recta que no conté el punt la directriu de la paràbola Té un eix de simetria que és la recta perpendicular que passa pel focus i que talla la paràbola en un punt anomenat vèrtex Referida a l’eix de simetria i a la seva perpendicular pel vèrtex, l’equació de la paràbola és y 2 =2 px , on p és la distància entre focus i directriu, anomenada paràmetre de la paràbola Hom pot demostrar que la gràfica de tota funció polinòmica de segon grau y= ax 2 + bx+ c és una paràbola de vèrtex - b /2 a ,…
anàlisi funcional
Matemàtiques
Estudi d’espais vectorials topològics els elements dls quals són funcions.
Els espais funcionals més interessants són els de les funcions contínues, el de les funcions integrables i el de les funcions normades Els principals conceptes de l’anàlisi, com la diferenciació i la integració, es poden generalitzar a espais de Banach donant lloc a estudis típics d’anàlisi funcional Té importants aplicacions a l’estudi d’equacions diferencials en derivades parcials, equacions funcionals i integrals, usant teoremes generals com el de Hahn-Banach, el de Riesz o el de l’apliació oberta
Claudi Alsina i Català

Claudi Alsina i Català (2024)
© Arxiu Família Alsina
Matemàtiques
Matemàtic.
Doctorat per la Universitat de Barcelona, feu estudis de postgrau a la Universitat de Massachusetts EUA Especialista en equacions funcionals, visualització, educació matemàtica, lògica difusa, geometria de Gaudí, metrologia catalana i en la divulgació de les matemàtiques Fou catedràtic de Matemàtiques de l’escola d’arquitectura de la Universitat Politècnica de Catalunya fins que es jubilà el 2016 Publicà una cinquantena de llibres —tant monografies tècniques com de divulgació—, i centenars d’articles de recerca i d’educació, i impartí conferències arreu del món Entre d’altres, exercí de …
hipèrbole
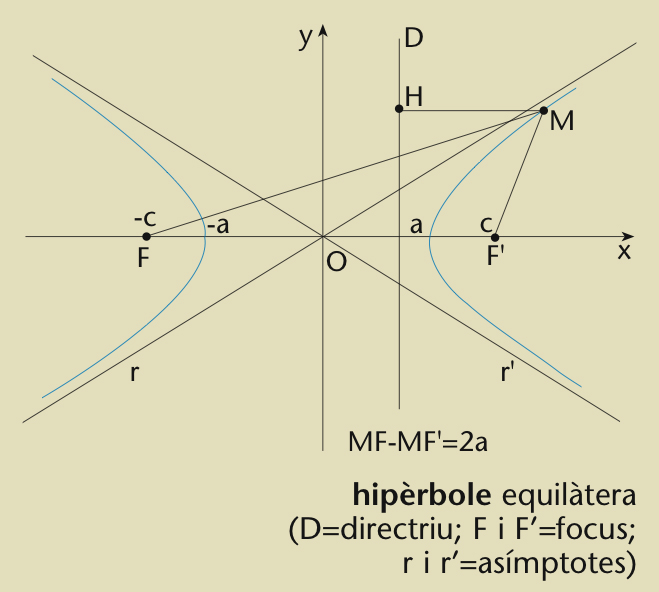
Hipèrbole equilàtera
© Fototeca.cat
Matemàtiques
Corba oberta, intersecció d’un con de revolució amb un pla que forma amb ’eix d’aquell un angle més petit que amb la generatriu.
Constitueix el lloc geomètric dels punts del pla tals que la diferència de llurs distàncies a dos punts fixos, anomenats focus , és una constant, simbolitzada habitualment per 2 a Té dos eixos de simetria i, referida a ells, la seva equació és x 2 / a 2 - y 2 / b 2 = 1, on i 2c és la distància entre els focus L’excentricitat e és c / a Les asímptotes són les rectes y = b / a x asímptota Quan a = b , la hipèrbola és anomenada equilàtera , i la seva equació referida a les asímptotes, que són perpendiculars, és y = k/ x la seva excentricitat és
arc
Matemàtiques
Segment o part d’una corba.
Usualment també designa una corba oberta completa Les característiques d’un arc llargada, corda, fletxa depenen de la corba a la qual pertany En el cas d’una circumferència, hom mesura els arcs en unitats d'angle i un arc val igual que l'angle en el centre que el limita en trigonometria, però, hom considera a vegades que un arc de circumferència α, mesurat en radians, admet una infinitat de determinacions que difereixen per un nombre enter de circumferències i són donades per la fórmula α + 2 k π, on k pot ésser zero o un enter qualsevol El principal problema que es planteja a…
corba
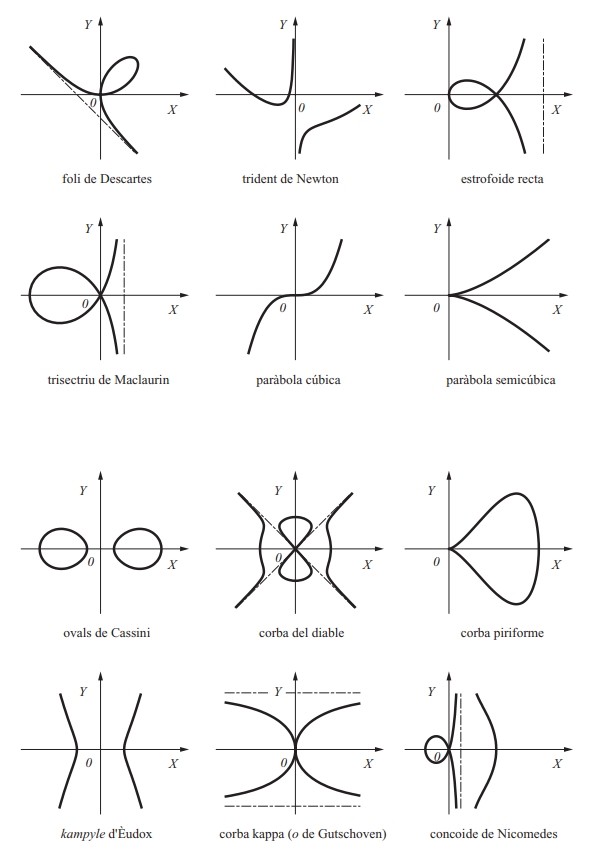
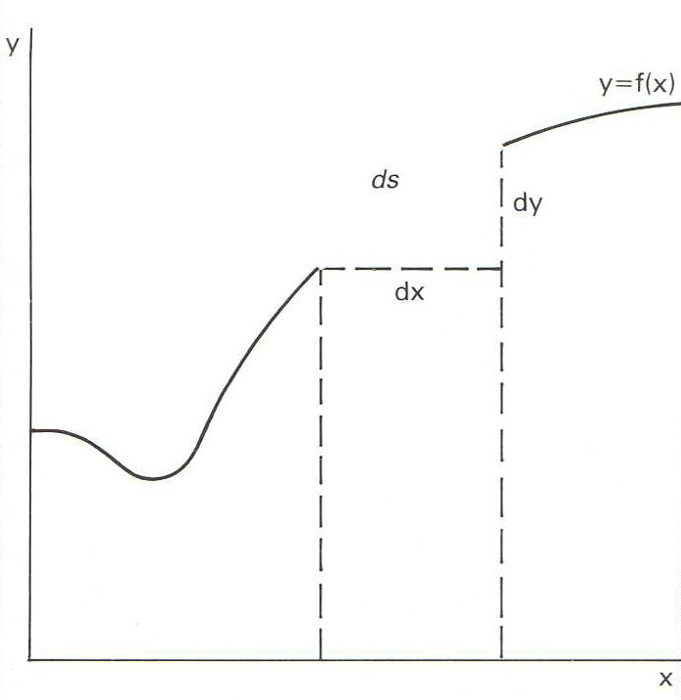
Corbes cúbiques i quàrtiques
Matemàtiques
Lloc geomètric que és la trajectòria d’un punt que es mou amb un sol grau de llibertat.
Una corba sempre pot ser considerada com una infinitat simple de punts, i aquest és el plantejament adoptat pels matemàtics en l’estudi de les corbes contínues topologia En aquest sentit, una corba és el conjunt de punts de ℝ n que és homeomorf amb un interval a , b ⊂ ℝ Seguint Menger hom podria considerar les corbes al pla espai com a objectes de dimensió topològica 1 ja que tota circumferència superfície esfèrica de centre un punt de la corba la talla en un conjunt de punts de dimensió zero punts que són centres de circumferències superfícies esfèriques que no contenen altres punts del…