Resultats de la cerca
Es mostren 32 resultats
agrupament de classes
Matemàtiques
Divisió de l’interval que comprèn totes les observacions d’una sèrie estadística en petits intervals iguals.
Cada un d’aquests intervals constitueix una classe, i hom atribueix el valor mitjà de l’interval a totes les observacions que conté El nombre d’observacions dins un interval és anomenat freqüència d’aquest interval
mitjana
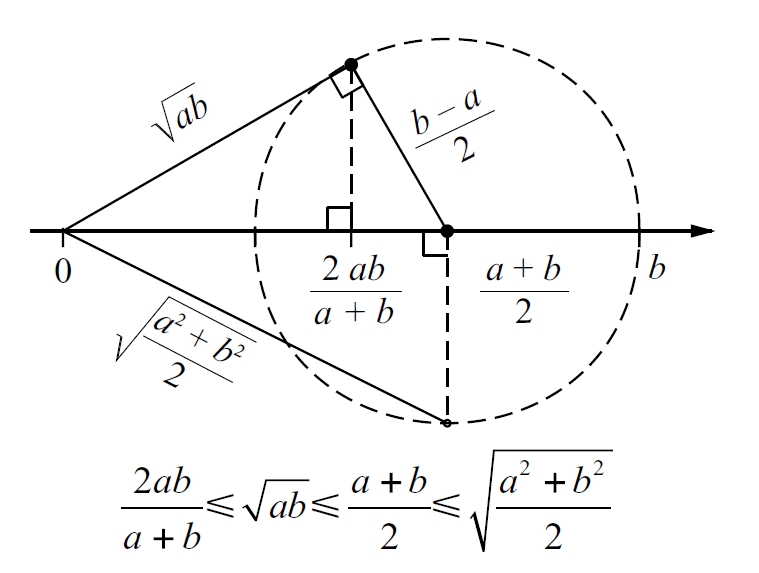
Mitjanes dels nombres a i b: harmònica, geomètrica, aritmètica i quadràtica
© fototeca.cat
Matemàtiques
Donats n valors o observacions x1, x2, ..., xn, valor x definit com la suma de tots ells dividida per llur nombre, és a dir, .
La mitjana x així definida és anomenada també mitjana aritmètica i valor mitjà Si les observacions constitueixen el conjunt de la població, x serà la mitjana de la població , mentre que si les observacions són d’una mostra aleatòria de la població mostreig, x és la mitjana de la mostra A la pràctica, la mitjana de la població és normalment desconeguda, i hom utilitza com a estimació la mitjana d’una mostra Quan les observacions poden ésser agrupades en k classes, amb efectius respectius n 1 , n 2 , , n k i freqüències respectives f 1 , f 2 , , f k , la…
teorema central del límit
Matemàtiques
Teorema segons el qual, per a una distribució de probabilitat arbitrària de mitjana μ i variància σ2, i essent x̄ la mitjana de n observacions independents d’aquesta distribució, la variable
té una distribució
.
Segons aquest teorema, per a n → ∞ la mitjana de n observacions independents segueix una llei normal de mitjana igual a la de la població i de variància igual a 1/ n de la d’aquesta A la pràctica, per a n ≥ 10 l’aproximació és ja suficient Aquest teorema, formulat per Lindeberg i Levi, és un dels més importants de la teoria de probabilitats De Moivre en feu la primera demostració el 1732 en el cas d’una distribució binomial, i posteriorment Ljapunov en demostrà la validesa molt general en cas de variables aleatòries Això explica per què a la pràctica hi ha moltes variables que…
test d’hipòtesis estadístiques
Matemàtiques
Donada una mostra de grandària n, ( x1,...,xn ), formada per n realitzacions o observacions independents d’un cert fenomen o experiment.
Aquest mètode permet de decidir, a partir de les dades observades, si una hipòtesi estadística que hom ha fet sobre el model probabilístic del fenomen és correcta o no ho és Aquesta decisió hauria d’ésser presa sempre amb un cert grau d’incertesa Els problemes que tracta de resoldre aquesta teoria poden ésser, per exemple, decidir quin dels dos mètodes diferents de fabricació de bombetes elèctriques dona una mida mitjana més gran, o bé saber, a partir d’una sèrie d’anàlisis, si un malalt té una certa malaltia Sovint el model probabilístic consisteix en una llei de probabilitat teòrica donada…
aberrància
Matemàtiques
Singularitat que es presenta quan els valors obtinguts d’un conjunt d’observacions d’una magnitud disten ostensiblement del valor mitjà obtingut amb totes les observacions.
Aquest terme és aplicat quan un nombre reduït de diversos fets presenten d’una manera excepcional unes característiques diferents d’altres fets que, dins el mateix cas, són relativament ben agrupats al voltant d’un valor mitjà
moda
Matemàtiques
Donat un conjunt de dades o observacions, valor de l’observació més freqüent.
És una característica de tendència central Pot donar-se el cas de l’existència de dos o més modes o valors modals en una mateixa distribució
prova de khi quadrat
Matemàtiques
Prova de significació emprada per a sèries grans d’observacions, que mesura l’acostament entre la distribució de les dites observacions i una distribució de freqüències teòricament establerta, dita de χ 2
.
Si F i designa les freqüències experimentals i P i les freqüències esperades teòricament, hom calcula la fidelitat de la distribució experimental envers la de χ 2 per mitjà de la fórmula χ 2 =0 en el cas de coincidència entre totes dues distribucions Hom sol emprar aquesta prova per al contrast d’hipòtesis, amb uns marges de fiabilitat del 95 o del 99%, i és aplicable a situacions molt diverses
Ṯābit ibn Qurra
Astronomia
Matemàtiques
Astrònom i matemàtic àrab.
Fou membre de l’escola científica de Ḥarrān i hi fou un dels principals traductors d’obres astronòmiques gregues Formulà la teoria de la trepidació dels equinoccis tot denunciant els errors existents en les observacions dels astrònoms grecs
Johann Tobias Mayer
Astronomia
Matemàtiques
Astrònom i matemàtic alemany.
Fou director de l’observatori de Göttingen En 1753-61 féu nombroses observacions dels moviments de la Lluna, publicades pòstumament el 1770 També elaborà un catàleg estellar d’un miler d’estels zodiacals El 1761 establí una fórmula per tal de poder calcular i corregir les desviacions instrumentals
Johannes Werner
Astronomia
Matemàtiques
Matemàtic i astrònom alemany, conegut també amb la forma llatinitzada de Vernerus.
Capellà a l’església de Sankt Johannes de Nuremberg, estudià la geometria, la geografia, l’astronomia, etc És un dels creadors de la trigonometria moderna Ideà un tipus de transformació algèbrica que anomenà prostafèresi , que fou usada fins la introducció dels logaritmes Féu nombroses observacions meteorològiques i astronòmiques