Resultats de la cerca
Es mostren 5 resultats
sinus d’un angle
Matemàtiques
Donats dos eixos perpendiculars x i y, i un segment de longitud unitat OP que forma un angle α amb l’eix d’abscisses x, valor de la projecció de OP sobre l’eix y
.
Aquesta projecció és el sinus de l’angle α i és denotada per sinα El sinus de l’angle α determinat entre dos segments qualssevol és el sinus de l’angle que, dibuixat sobre aquest cercle goniomètric, té la mateixa obertura que α Algunes fórmules trigonomètriques relatives al sinus d’un angle són sinα+β = sinα cosβ - cosα sinβ sin-α = -sinα sinα sinβ = cosα-β - cosα+β/2 sinα + sinβ = 2 sinα+β/2 cosα-β/2 Entre el cosinus i el sinus d’un angle hi ha la relació fonamental cos 2 α+sin 2 α=1
cosinus d’un angle
Matemàtiques
Donats dos eixos perpendiculars x
i y
, i un segment de longitud unitat OP
que forma un angle α amb l’eix d’abscisses x
, valor de la projecció de OP
sobre l’eix x
.
Aquesta projecció és el cosinus de l’angle α i és denotada per cos α El cosinus de l’angle α determinat entre dos segments qualsevol és el cosinus de l’angle que, dibuixat sobre aquest cercle goniomètric, té la mateixa obertura que α Algunes fórmules trigonomètriques relatives al cosinus d’un angle són cosα+β=cosα cosβ-sinα sinβ cos-α= cosα cosαcosβ = cosα+β+cosα-β/2 cosα + cosβ = 2 cosα + β/2cosα - β/2 Entre el cosinus i el sinus d’un angle hi ha la relació fonamental cos 2 α + sin 2 α = 1
asímptota
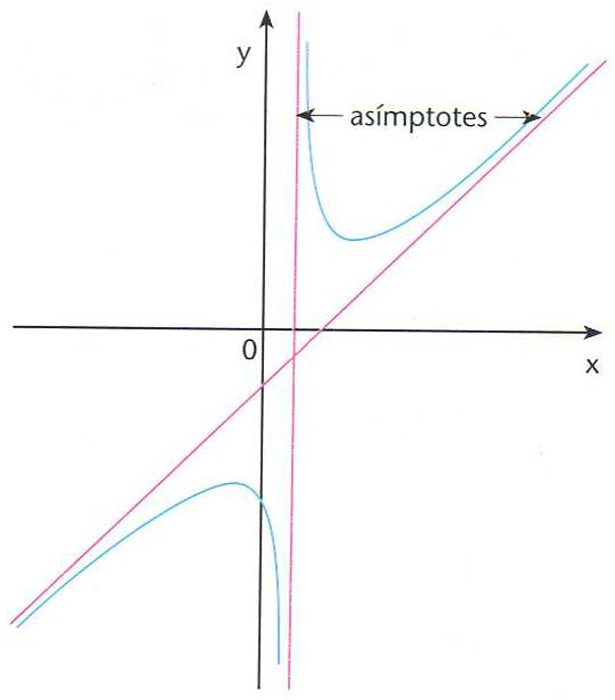
Asímptotes
Matemàtiques
Recta a la qual s’acosta un punt variable sobre una branca de corba quan el punt s’allunya cap a l’infinit.
Per a poder afirmar que una branca de corba té una asímptota cal que, si el punt P es mou sobre aquesta de manera que la distància de P a l’origen de coordenades O creix infinitament, la direcció de la recta OP tingui un límit determinat Hom troba aquest límit per mitjà del quocient y/x = tg a Coneguda la direcció de l’asímptota, hom determina la seva ordenada a l’origen per la condició que la distància entre dos punts que tinguin igual abscissa, un sobre la corba, l’altre sobre l’asímptota, tingui límit zero quan aquella abscissa comuna es fa infinita Així, per exemple, la…
categoria
Matemàtiques
Estructura algèbrica composta per una família d’objectes matemàtics i per una família de morfismes entre aquests objectes, tal que satisfà les següents propietats.
per a tot parell X,Y d’objectes de la categoria existeix un conjunt Hom X,Y, anomenat conjunt de morfismes de X en Y, tal que HomX,Y = HomX’,Y’ si i només X=X’ i Y=Y’ i, per a tot triplet X,Y,Z d’objectes de la categoria, existeix una aplicació Hom Y,Z x HomX,Z→HomX,Z, anomenada composició de morfismes, que satisfà l’associativitat i l’existència d’una identitat a cada HomX,X és a dir, existeix un morfisme 1 x tal que per a tot f de HomX,X se satisfà Els objectes d’una categoria no han de formar necessàriament un conjunt, sino una classe així, per exemple, la categoria dels grups G r és…
trigonometria

1, circumferència de referència per a la definició de les raons trigonomètriques; 2, representació gràfica de les línies trigonomètriques; 3, símbols emprats en la resuloció de triangles
© fototeca.cat
Matemàtiques
Part de la matemàtica inicialment dedicada a l’estudi de les relacions entre les amplituds dels angles i les longituds dels segments que llurs costats determinen en les rectes que tallen.
La trigonometria es basa en les propietats de les anomenades raons trigonomètriques , que són definides a partir d’un punt P x,y d’una circumferència de centre O i per l’angle α que forma el radi r = OP amb l’eix OX , mitjançant els sis quocients següents sin α = y/r sinus cos α = x/r cosinus tg α = y/x tangent cotg α x/y cotangent sec α = r/x secant cosec α = r/y cosecant Quan el punt P és a una distància r = 1 de l’origen O , el valor absolut d’aquestes raons és representat per la longitud de certs segments anomenats línies trigonomètriques , respectivament, fàcils de traçar…