Resultats de la cerca
Es mostren 14 resultats
oval de Descartes
Matemàtiques
Corba plana que, en coordenades bipolars, té l’expressió ar+br’=c, on a, b i c són reals que satisfan a≠0 i b≠0, i r i r’ són les coordenades bipolars.
L’ellipse i la circumferència en són casos particulars
anàlisi harmònica
Matemàtiques
Representació de funcions periòdiques mitjançant sumació i integració de desenvolupaments en sèrie d’algunes funcions trigonomètriques elementals.
Permet d’obtenir expressions senzilles aproximades de les funcions i deduir propietats generals a partir de les propietats particulars d’aquelles funcions elementals
distribució gamma
Matemàtiques
Llei de probabilitat de la variable contínua x, la funció de densitat de la qual és f(x) = e- xxk - 1/Γ(k) (0 < x < ∞;k > 0).
D’aquesta llei deriven algunes expressions particulars, com la llei X 2 i la llei d’Erlang Tendeix cap a la llei normal quan k augmenta indefinidament
Diofant d’Alexandria
Matemàtiques
Matemàtic grec.
Els seus escrits sobre àlgebra, amb un estil d’exposició marcadament analític que el vincula estretament amb els treballs dels babilonis, contribuïren de forma essencial al perfeccionament de la notació algèbrica i a l’establiment de noves vies d’investigació En la seva obra cabdal, Aritmètica , estudià una àmplia sèrie de problemes numèrics limitant-se, en general, a trobar-hi solucions particulars mitjançant algun mètode de càlcul i admetent només com a solucions els nombres enters i racionals positius La seva obra influí en el posterior desenvolupament de la geometria…
integral múltiple
Matemàtiques
Integral definida sobre un domini D de ℝn.
Donat un domini D de ℝ n , i una partició en dominis elementals D i d’àrees a i i diàmetres d i , i donada una funció real definida sobre D , fD ⊂ ℝ n → ℝ, límit I quan els d i tendeixen a 0, de les sumes de Riemann on A i ∈ D i Hom diu que I és la integral de f en D i és notada per ʃ ʃ n ʃ D ʃ x 1 , x n d x 1 dx n Els casos particulars n =2 i n =3 constitueixen la integral doble i la integral triple, respectivament Les integrals múltiples poden ésser calculades per integració unidimensional reiterada
teorema de Pitàgores
Matemàtiques
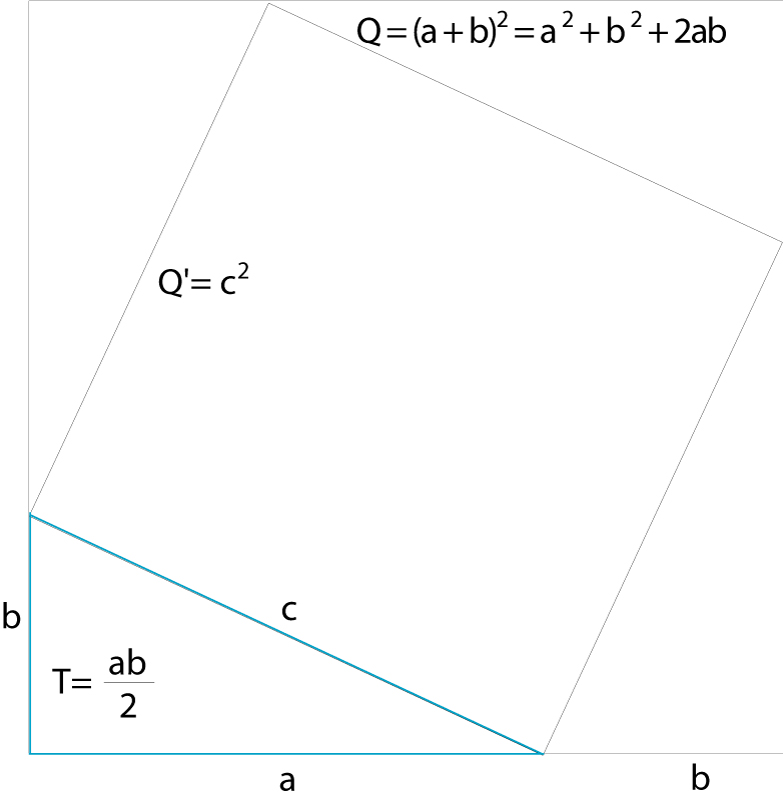
Teorema fonamental de la geometria segons el qual en un triangle rectangle l’àrea del quadrat que té per costat la hipotenusa és igual a la suma de les àrees dels quadrats que tenen per costat els catets.
Si a i b representen les longituds dels catets i c la longitud de la hipotenusa, el teorema Pitàgores és expressat per la igualtat c 2 = a 2 + b 2 Bé que la primera demostració del teorema sembla que fou feta pels membres de l’ escola pitagòrica Pitàgores vers l’any 550 aC, el teorema de Pitàgores, almenys en alguns casos particulars, ja era conegut pel poble egipci vers l’any 2000 aC, pels xinesos vers l’any 1100 aC i pels vedes vers l’any 800 aC D’altra banda, fou a partir del teorema que els pitagòrics descobriren que no n'hi ha prou amb els nombres enters i fraccionaris…
espai topològic
Matemàtiques
Conjunt X en el qual s’ha donat una topologia
.
Els conjunts de la família donada són anomenats oberts , i llurs complementaris, tancats Rep el nom d' entorn obert d’un punt tot conjunt obert que el conté Base de l’espai topològic és una família de conjunts oberts que per reunió poden donar qualsevol altre obert Alguns espais topològics tenen llur topologia definida per mitjà d’una distància, la qual determina la base d’oberts de la topologia formada per les boles o esferes En són exemples la recta real ℝ i els espais euclidians de dimensions superiors ℝ n Un subespai d’un espai topològic és una part de l’espai amb la topologia induïda…
equació diferencial
Matemàtiques
Equació funcional (en el sentit que les incògnites són funcions) on apareixen les derivades de la funció incògnita.
Si la funció és d’una sola variable, l’equació és una equació diferencial ordinària Per tal que aquesta definició, molt general, no inclogui certes classes d’equacions especials com és ara les equacions diferencials en diferències f ´ x = f x + h , hom precisa que la funció incògnita i les seves derivades tan sols poden ésser sotmeses a operacions algèbriques El tipus general d’equació diferencial és escrit F t,x,x´,,x n = 0 Hom defineix l' ordre d’una equació diferencial com el de la màxima derivada que apareix en l’equació Si F té forma polinòmica, hom parla de grau de l’equació…
equació diferencial de Bessel
Matemàtiques
Nom donat a l’equació diferencial x2y’’ + xy’ + (x2-ν2)y = 0, essent ν un nombre complex qualsevol.
Resulta d’expressar l’equació de Laplace, ∇ 2 ψ x, y, z = 0, en coordenades cilíndriquesquan és possible d’aplicar a la funció ϕ el mètode de separació de variables ϕ x , y , z = X x Y y Z z Una sollució particular de l’equació de Bessel és la funció de Bessel de primera classe , d’ordre ν on Γ és la funció gamma J - ν x n'és també solució particular Si n és enter, la corresponent funció J n x pot ésser estesa a tot ℂ si ν no és enter, J ν x pot ésser estesa a ℂllevat de l’eix real negatiu Si n és enter, J - n x = -1 n J n x en canvi, si ν no és enter, J ν x i J - ν x…
abstracció matemàtica
Matemàtiques
Abstracció d’una propietat o d’un concepte passant d’un cas particular a un cas més general, o generalitzant un concepte a partir de l’observació de propietats comunes i de no tenir en compte les diferències entre els casos particulars.