Resultats de la cerca
Es mostren 44 resultats
potència
Matemàtiques
Caràcter comú de dos conjunts entre els elements dels quals hom pot establir una correspondència bijectiva.
Dos conjunts de la mateixa potència són equipotents
potència
Matemàtiques
Donats un nombre a
, anomenat base
, i un nombre natural n
, anomenat exponent
, producte
a n
de n
factors iguals a a
, és a dir,
.
Hom generalitza la noció de potència al cas en què l’exponent és un enter negatiu, mitjançant la fórmula a -n =1/a n , i al cas en què l’exponent és un nombre racional, mitjançant la fórmula La generalització al cas que l’exponent sigui un nombre real qualsevol té lloc mitjançant la funció exponencial , i en el cas que l’exponent sigui un nombre complex, mitjançant la fórmula de De Moivre Les propietats més importants de les potències són
potència tensorial
Matemàtiques
La potència tensorial T p
( E
) és el producte
, amb
E i
per a cada i
= 1,..., p
.
potència d’un conjunt
Matemàtiques
Conjunt OOO(X) els elements del qual són els subconjunts del conjunt X.
La seva existència és garantida per l’axioma de les parts, que és un dels axiomes de la teoria axiomàtica de conjunts És anomenat també el conjunt de parts d' X El nom de conjunt potència prové del fet que, si acceptem l’axioma de l’elecció, el cardinal del conjunt OOO X és 2 card x
base d’una potència
Matemàtiques
Nombre que caldrà prendre com a factor tantes vegades com indica l’exponent amb què és afectat: a 13 4
, 13 és la base i 4 l’exponent.
base d’una potència
Matemàtiques
Factor que cal multiplicar per ell mateix tantes vegades com indica l’exponent.
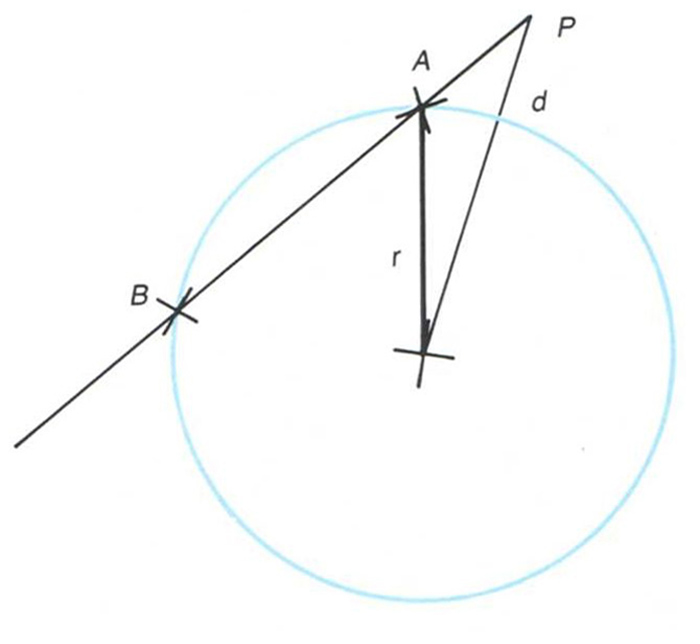
potència d’un punt respecte a una circumferència
fototeca.cat
©
Matemàtiques
Donats un punt P
i una circumferència, producte de les distàncies del punt P
als dos punts A
i B
que una recta que passa per P
determina sobre la circumferència.
Es verifica que el dit producte, és independent de la recta traçada fototecacat ©