Resultats de la cerca
Es mostren 9 resultats
mostra
Matemàtiques
Porció finita d’una població que és utilitzada per a extrapolar conclusions sobre diverses característiques de la població total.
En general, l’elecció d’una mostra estadística és duta a terme amb bases aleatòries, puix que tots els elements de la població han de gaudir de la mateixa probabilitat de formar part de la mostra, les dimensions de la qual són molt variables i depenen de les característiques pròpies del poblema que estadísticament hom vol estimar En mesurar una característica en una mostra hom obté els valors mostrals o distribució empírica de la mostra, de la qual hom extreu els paràmetres estadístics essencials, és a dir, la mitjana, la variància, la mediana, etc, que són els que permeten d’extreure…
perspectiva central
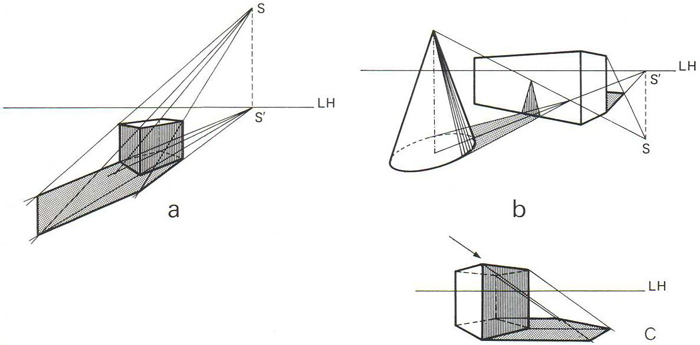
Ombra pròpia i ombra llançada projectades pel Sol (S) (projecció de la llum solar). LH essent la línia de l’horitzó i S’ el punt de fuga, quan és situat davant l’espectador (a), darrere l’espectador (b) i al costat de l’espectador (c)
© fototeca.cat
Art
Disseny i arts gràfiques
Matemàtiques
Sistema de representació les línies projectants del qual passen per un punt fix anomenat centre de projecció
o pol
.
Variants d’aquest tipus de perspectiva són la perspectiva cònica i la projecció de la llum el centre d’aquesta projecció és el focus o punt lluminós, que pot ésser a una distància finita dels cossos que illumina, i en aquest cas els raigs són divergents llum artificial , o infinita, i aleshores els raigs són parallels llum solar Ombres pròpies i ombres llançades projectades pel focus F projecció de llum artificial, F’ essent els punts de fuga © fototecacat
semblança
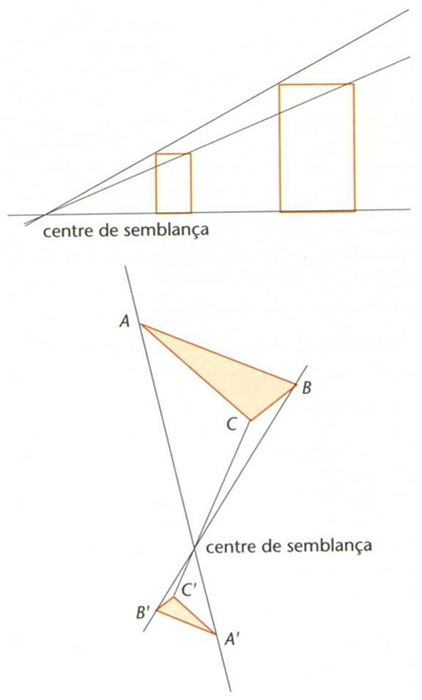
Dues semblances directes
© Fototeca.cat
Matemàtiques
Transformació geomètrica T de ℝn en ℝn tal que la distància entre les imatges de dos punts qualssevol és igual a la distància entre aquests dos punts multiplicada per una quantitat constant positiva dita raó de la semblança.
És a dir, d T x, T y = k, d x, y Dues figures són anomenades semblants si hi ha una semblança que transforma l’una en l’altra Les semblances conserven la forma de les figures però en canvien la grandària, eixamplant-la o reduint-la segons que la raó sigui respectivament major o menor que 1 Les semblances de raó 1 són dites isometries o moviments rígids , els quals són sempre el resultat de compondre una translació amb una transformació lineal ortogonal que conserva els angles Les homotècies són exemples típics de semblances Tota semblança és el resultat d’aplicar successivament una…
fiabilitat
Matemàtiques
Tecnologia
Mesura de la confiança que hom pot tenir en el funcionament correcte d’un sistema o d’un dels elements que el componen.
Hom l’expressa per la probabilitat que s’acompleixi aquest funcionament correcte durant un temps determinat i en condicions especificades de funcionament La fiabilitat variarà amb aquestes condicions, tant si són pròpies del sistema com si són externes Hom pot estudiar la fiabilitat d’un element i la del sistema en el seu conjunt en funció del temps mitjançant tres nocions interrelacionades la supervivència, la duració de vida i la probabilitat condicional de falliment o d’avaria, la més instructiva de les quals és la tercera amb un nombre suficient d’observacions hom obté, per a…
cònica
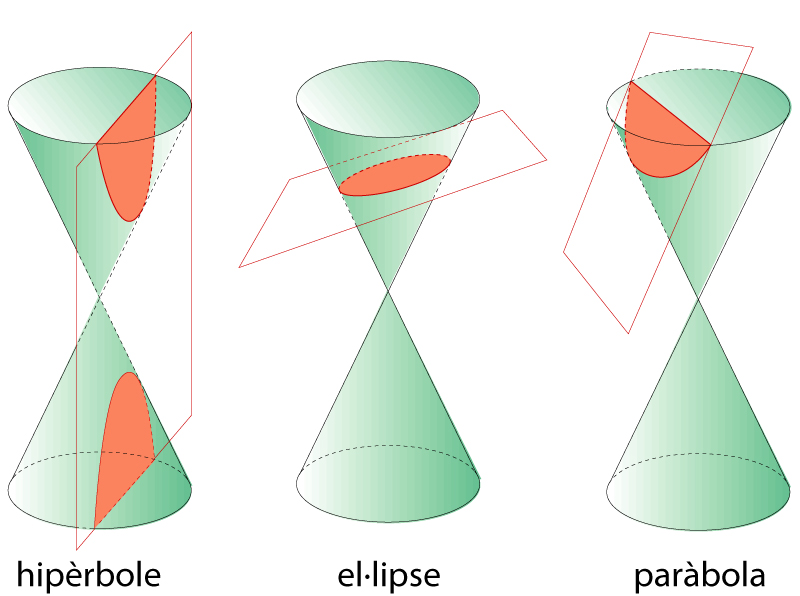
Còniques com a secció de cons
© Fototeca.cat
Matemàtiques
Corba de segon grau en un pla.
El primer estudi conegut sobre còniques és el tractat d’Apolloni de Perge, que les definia com a possibles seccions d’un con Projectivament, hom defineix la cònica com a lloc geomètric dels punts dobles d’una polaritat L’estudi afí de les còniques destaca els següents elements centre , que és el pol de la recta de l’infinit, diàmetre , qualsevol recta que passa pel centre, asímptotes , els diàmetres tangents a la cònica En l’estudi euclidià hom distingeix, a més, els eixos principals, que són una parella de diàmetres perpendiculars i també conjugats respecte a la polaritat induïda per la…
teorema de Bonnet
Matemàtiques
Teorema segons el qual els coeficients de les formes fonamentals d’una superfície determinen localment la parametrització de la superfície, llevat de composició amb transformacions ortogonals pròpies i translacions.
Concretament, si E , F , G , e , f , g són funcions diferenciables definides en un obert V ⊂ ℝ 2 , amb E > 0, G > 0 i EG – F 2 > 0 tals que satisfan les equacions de compatibilitat de Gauss i de Mainardi-Codazzi, aleshores per a cada q ∈ V existeix un entorn U ⊂ V de q i un difeomorfisme x U → x U ⊂ ℝ 3 tal que la superfície regular x U ⊂ ℝ 3 té E , F , G , e , f , g per coeficients en les seves formes fonamentals Amés, si U és connex i x’ U → x’ U ⊂ ℝ 3 és un altre difeomorfisme que satisfà les mateixes condicions, aleshores existeix una translació T i una transformació…
Esteve Terradas i Illa

Esteve Terradas i Illa (al centre) amb la junta de la Societat Astronòmica de Barcelona
© Fototeca.cat
Matemàtiques
Enginyer industrial i de camins i matemàtic.
Estudià a Charlottenburg Berlín, Barcelona i Madrid Es doctorà també en ciències exactes i físiques i fou professor de les universitats de Saragossa, Barcelona i Madrid S’especialitzà en ciències fisicomatemàtiques, publicà nombrosos articles sobre aquests temes i el 1909 llegí a l’Acadèmia de Ciències i Arts de Barcelona una memòria destacada Emisión de radiaciones por cuerpos fijos o en movimiento També exercí una activitat pedagògica important Publicà articles en la Revista de la Academia de Ciencias , de Madrid, i en el butlletí de l’Institut de Ciències de Barcelona Fundà un seminari…
Jacint Feliu i Utzet

Jacint Feliu i Utzet
© Escola Pia
Matemàtiques
Cristianisme
Religiós escolapi, matemàtic i restaurador de l’orde a l’Estat espanyol.
Biografia Alumne avantatjat de la classe d’aritmètica del pare Francesc Ferrer a l’Escola Pia de Santa Anna El 2 d’agost de 1802 ingressà al noviciat a Moià i hi professà el 26 de desembre de 1804 El 1810, per evitar la guerra del Francès, es refugià a Mallorca, on collaborà amb dos escolapis més en la fundació d’un collegi a Palma Entrà en contacte amb l’Acadèmia Militar de Palma, on començà a impartir algunes assignatures Quan l’Acadèmia es traslladà a Gandia i després a València, hi continuà com a professor de matemàtiques El 1823 el Govern monàrquic restablert clausurà les acadèmies i el…
Aristòtil

Còpia romana d’Aristòtil del període imperial (segle I o II dC) d’un bronze perdut realitzat per Lísip (Museu del Louvre)
Yuxuan Wang (CC BY-NC-ND 2.0)
Filosofia
Matemàtiques
Filòsof i científic grec, un dels esperits més potents i influents de la història.
Vida i obra Del clan dels asclepíades, era fill de Nicòmac, metge i amic d’Amintes II de Macedònia A divuit anys ingressà a l’Acadèmia Els primers temps fou el deixeble predilecte de Plató, però les divergències posteriors els distanciaren A la mort del mestre 347, Aristòtil abandonà Atenes i passà tres anys a Assos, on s’uní amb Herpillis, de la qual tingué un fill, Nicòmac, al qual dedicà un dels tractats d’ètica D’Assos passà a Mitilene d’aquesta època daten molts dels seus treballs de biologia En 343-342 aC Filip de Macedònia li encarregà l’educació d’Alexandre Aristòtil, que atribuïa una…