Resultats de la cerca
Es mostren 6 resultats
altura
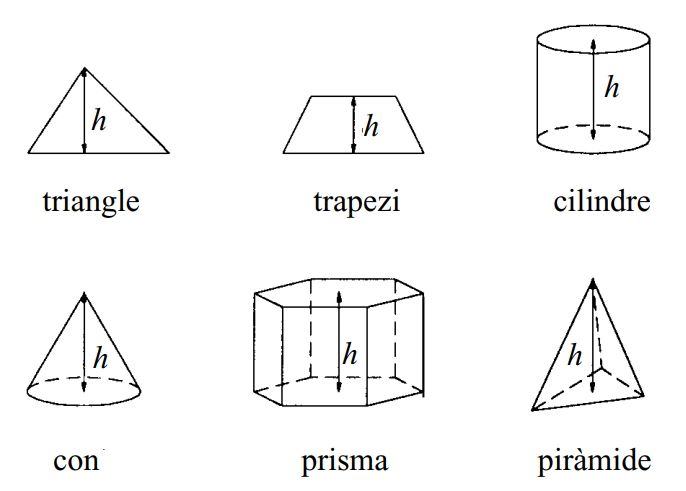
Altures de diferents figures i cossos geomètrics
© Fototeca.cat
Matemàtiques
Segment de recta (o també la seva longitud) en les figures i en els cossos geomètrics comprès entre dos de llurs elements (un vèrtex i un costat al triangle, dos costats al paral·lelogram) i perpendicular almenys a un d’aquests elements, anomenat base, o bé a una recta o a un pla que els determini.
Moltes figures i molts cossos presenten diverses altures segons quin costat hom prengui com a base En un triangle, les tres altures es tallen en un punt dit ortocentre i els seus peus determinen el triangle òrtic
variable aleatòria
Matemàtiques
Aplicació mesurable d’un espai de probabilitat (Ω, A, P) en (ℝ, Bℝ), on ℝés el conjunt dels nombres reals i Bℝ la tribu de Borel corresponent.
Expressa el resultat d’un experiment aleatori En el cas que la funció prengui un nombre finit de valors en tot interval finit, hom diu que es tracta d’una variable aleatòria discreta en el cas contrari, la variable aleatòria és de tipus continu Si X és una variable aleatòria del tipus continu tal que la seva funció de distribució admet una densitat fx , hom té σ 2 X = ∫ ℝ x- E X 2 f x dx
funció de distribució
Matemàtiques
Funció associada a una variable aleatòria que dona les probabilitats que aquesta prengui uns certs valors determinats.
Per a cada nombre real x , la funció de distribució F X pren el valor F X x = P {ϖ| X ϖ ≤ x } = P X ≤ x format per tots els esdeveniments elementals tals que el valor X ϖ no ultrapassa x Les propietats més importants que compleix la funció de distribució són si X és una variable aleatòria i F X la seva funció de distribució, sempre que x 1 < x 2 hom tindrà que F X x 1 ≤ F X x 2 si F X és una funció de distribució d’una variable aleatòria X , i si F X és la funció de distribució d’una variable aleatòria X , Les principals funcions de distribució són la distribució binomial ,…
sensedades
Matemàtiques
Valor convencional que s’assigna a una variable de la qual no es tenen dades, a fi d’evitar que prengui un valor per defecte o que quedi sense valor.
condicions inicials
Física
Matemàtiques
Donada una equació diferencial, condicions que cal imposar a la solució general per tal que prengui, ella i les seves derivades, uns determinats valors per a un valor especificat de la variable independent.
Les condicions inicials permeten, doncs, de determinar la solució particular del problema en ajustar les constants arbitràries de la solució general Per exemple, en el problema del moviment d’una massa puntual, un cop conegudes les forces que hi actuen, el moviment concret que realitza depèn només de la posició i la velocitat en un instant inicial, x t o i v t o , essent aquestes les condicions inicials del problema
condicions de contorn
Física
Matemàtiques
Donada una equació diferencial, condicions que cal imposar a la solució general per tal que prengui uns determinats valors en punts o zones concrets del domini de valors de la variable independent, zones anomenades contorns del problema.
Per exemple, el potencial electroestàtic d’una distribució de càrregues elèctriques ha de satisfer l’equació diferencial de Laplace ∇ 2 V =0 amb la condició de contorn que V sigui constant sobre la superfície dels conductors que hi hagi a l’espai del problema Les condicions de contorn són imposades per les lleis físiques, per la simetria o per la disposició experimental del problema Si el problema dinàmic és controlat per una o diverses equacions diferencials en derivades parcials, la solució particular del problema generalment ha de satisfer, a més d’unes condicions de contorn, unes…