Resultats de la cerca
Es mostren 11 resultats
funció primitiva d’una funció
Matemàtiques
Donada una funció f(x), funció F(x) tal que F´(x)=f(x) (on F´(x) és la derivada de la funció F(x)).
Hom diu aleshores que F x és la funció primitiva o, simplement, la primitiva, de f x Les primitives d’una funció són obtingudes mitjançant la determinació de la integral indefinida d’aquesta, F x =∫ x a f t
primitiu | primitiva
Matemàtiques
Donada una funció g, dit de la funcióf tal que la derivada de fés igual a g, és a dir, f = g (funció primitiva d'una funció).
primitiu | primitiva
Matemàtiques
En una teoria matemàtica, dit de cadascun dels objectes matemàtics inicials que són caracteritzats només pels axiomes de la teoria. Així, per exemple, els punts, les rectes i els plans són els elements primitius de la geometria de Hilbert.
integral indefinida

Integrals indefinides de les funcions usuals
©
Matemàtiques
Donada una funció f:(a,b] ⊂ℝ→ℝ, funció F definida en [a,b] per la integral (definida) F(x)= ∫fxsup;a&(t)dt.
Aquesta funció és una funció primitiva de la funció f , per tal com la seva derivada és igual a f , F' x = f x , i, de fet, genera la resta de funcions primitives de f , G x = F x + C , essent C una constant
funció de Heaviside
Matemàtiques
Funció H(x) real de variable real definida per .
És anomenada també funció esglaó o esglaó unitat de Heaviside És emprada en casos en què una magnitud passa bruscament de 0 a un valor constant no nul Les propietats de H x , determinades per Heaviside, han donat lloc a la teoria de distribucions distribució En aquest context, hom pot considerar-la la primitiva de la delta de Dirac
obert | oberta
Matemàtiques
En un espai mètric E, dit del conjunt C tal, que donat un punt qualsevol a de C existeix una distància d tal, que tots els punts de E situats a una distància del punt a inferior a d pertanyen al conjunt C.
Així, entre els intervals de la recta real, els únics oberts són els intervals oberts interval Les propietats formals dels conjunts oberts han conduït a la formulació de l’anomenada topologia general , en la qual la noció d’obert és una noció primitiva que només és subjecta als tres axiomes següents el conjunt buit és obert, tota unió de conjunts oberts és un conjunt obert, i tota intersecció finita de conjunts oberts és un conjunt obert
mesura
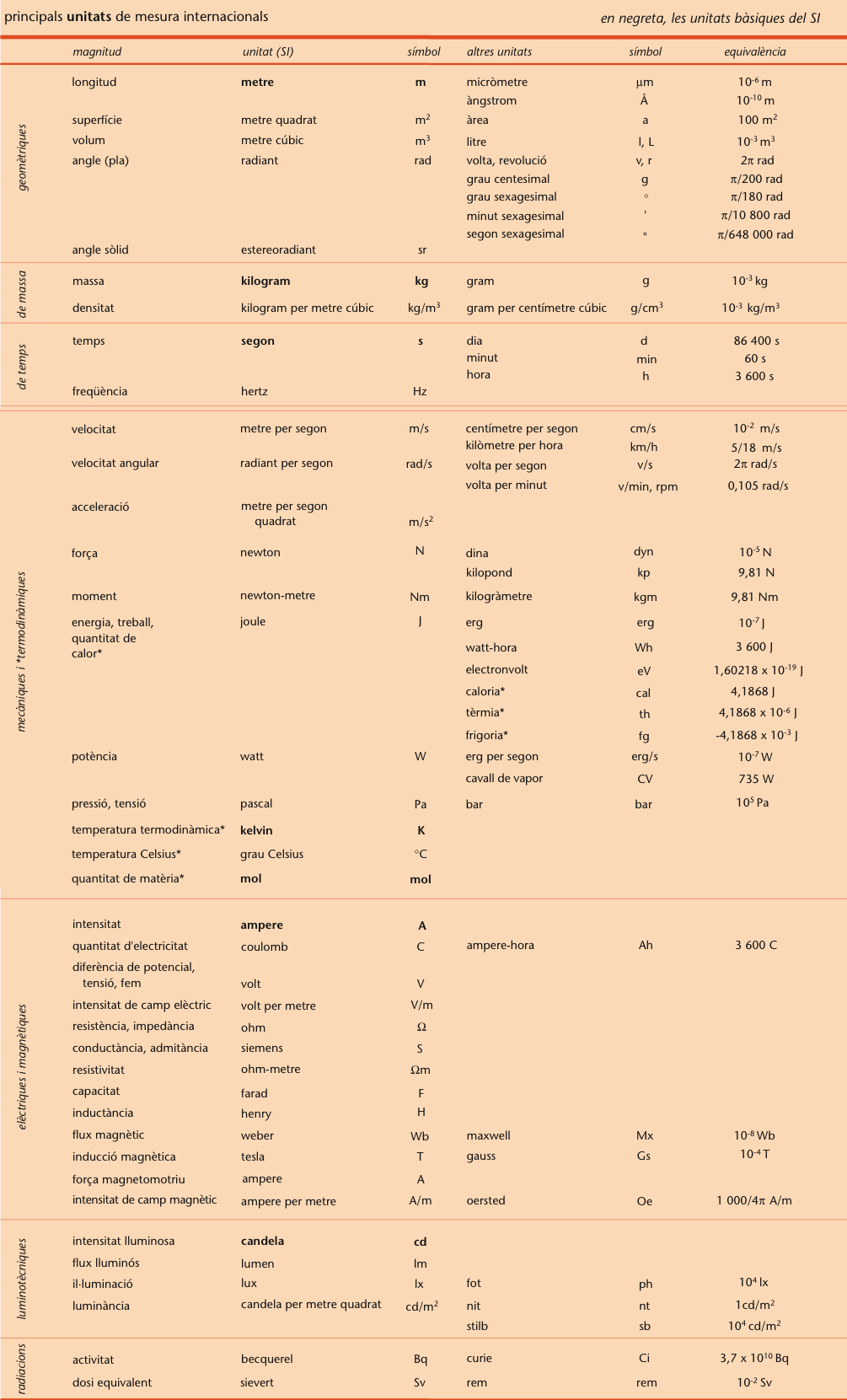
Principals unitats de mesura internacional
© Fototeca.cat
Física
Matemàtiques
Valor numèric obtingut experimentalment com a resultat d’un mesurament consistent a comparar una magnitud amb una altra de la mateixa espècie elegida com a unitat
, amb la finalitat d’establir unes relacions o la deducció d’unes conclusions.
Certes mesures, però, poden ésser de tipus qualitatiu “sí o no”, “més gran que o igual a”, “lineal”, etc, o poden estar relacionades amb una entitat gràfica d’imatge que serà donada per una “concentració” o per una probabilitat obtinguda per repetició del fet experimental El procés de mesura ha d’ésser objectiu i, per tant, la comparació ha d’ésser feta amb una magnitud unitat de la mateixa espècie i de similar dimensió Si hom l’efectua per un procés indirecte transductor, la magnitud final ha d’ésser calibrada en unitats de la magnitud primitiva No totes les magnituds són…
integració
Matemàtiques
Càlcul d’una integral.
Per a calcular integrals indefinides són útils, sovint, el mètode d’integració per substitució i el mètode d’integració per parts Segons el primer, hom fa x = φ t , i substitueix aquest valor a la integral ∫ f x dx = ∫fϕ t ϕ´ t dt , a fi de resoldre aquesta darrera més fàcilment El mètode d’integració per parts es basa en la relació → u dv = uv - que sigui de fàcil resolució Trobada la funció primitiva F x , la solució és ∫ f x dx = F x + C , on C és una constant La regla de Barrow proporciona un mètode general per a calcular integrals definides a partir de les…
regla de Barrow
Matemàtiques
Regla que s’utilitza per a calcular integrals definides segons la qual el valor d’una integral definida és la diferència entre els valors que pren una primitiva de la funció integrant en els extrems de la integral.
integral
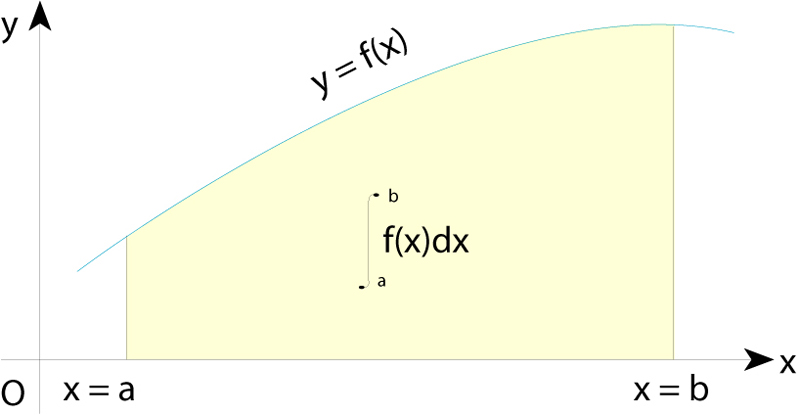
El valor d’una integral definida és igual a l’àrea limitada per la funció, l’eix d’abcisses i les dues ordenades corresponents als extrems de l’interval de definició
© Fototeca.cat
Matemàtiques
En el sentit més general, forma lineal μ sobre certs espais vectorials de funcions, que assigna a cada funció f de l’espai un escalar μ(f) anomenat integral de f.
Hom distingeix entre tres tipus fonamentals d’integral, la integral de Riemann , la integral de Riemann-Stieltjes i la integral de Lebesgue La integral de Riemann té una interpretació geomètrica simple per tal com fou definida a fi de calcular àrees i volums de figures geomètriques Si a,b és un interval tancat de la recta real, i P={ x 0 ,, x n } és una partició de a,b , és a dir, un conjunt finit de punts tal que a = x 0 ≤ x 1 ≤ ≤ x n = b , sigui Δ x i = x i - 1 per a i =1,, n Si f és una funció fitada definida en a, b , hom determina en cada subinterval x i - 1 , x i els termes M i…