Resultats de la cerca
Es mostren 4 resultats
teorema de Green
Matemàtiques
Teorema segons el qual, sota condicions força generals, si f i g són dues funcions definides en un recinte de l’espai i V és una regió interior a aquest recinte limitada per una superfície S, es compleix: .
on ∇ 2 = ∂ 2 /∂ x 2 + ∂ 2 /∂ y 2 + ∂ 2 /∂ z 2 és el laplacià, i ∂/∂ n és la derivada direccional segons la normal a la superfície dirigida cap a fora, és a dir, ∂ f /∂ n = ∇ f n
element de superfície
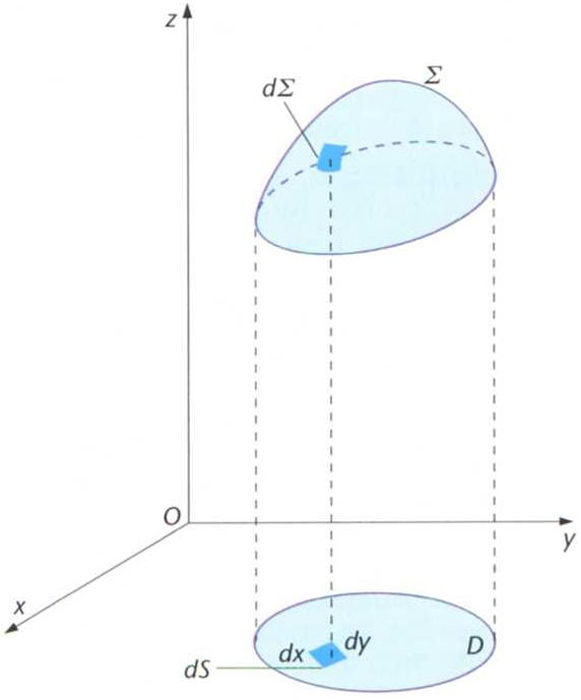
Element de superfície
© fototeca.cat
Matemàtiques
Cadascuna de les parts infinitesimals en què hom divideix una superfície a l’hora de calcular-ne l’àrea.
En coordenades cartesianes l’element de superfície dS val dS = dx dy , i en coordenades polars dS = ρ d ρ d θ L’àrea A d’una superfície regular z = f x,y que tingui com a projecció en el pla XOY un recinte S , és igual a la integral doble expressada per
volum
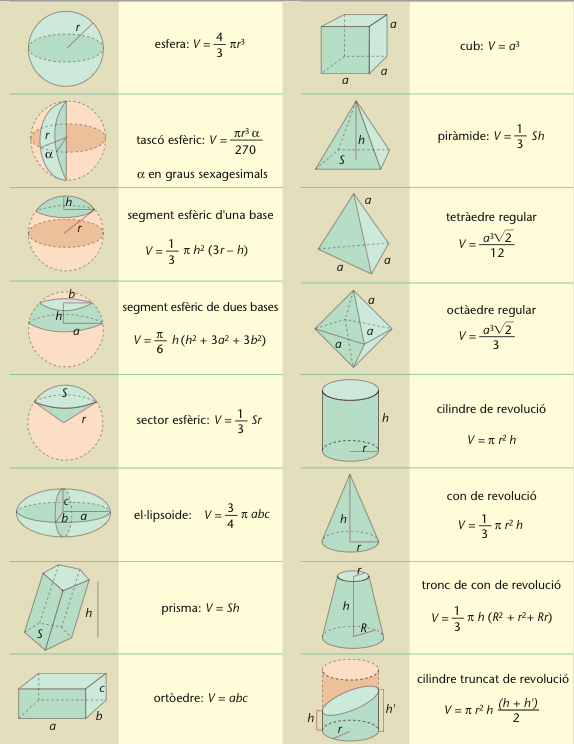
Fórmules per al càlcul de volums
© Fototeca.cat
Matemàtiques
Grandor o mesura de la porció de l’espai ocupada per un cos.
El volum és una mesura que a tota regió de l’espai de tres dimensions assigna un nombre real positiu, de manera que es compleix la propietat additiva, és a dir, que el volum d’un cos és igual a la suma dels volums de qualsevol partició que hom hagi fet en el cos divisió del cos en parts disjuntes Prenent com a base que el volum assignat a un cub de costat a és a 3 , el volum de qualsevol altre cos pot ésser calculat com l’ínfim de la suma dels volums dels cubs disjunts que plegats cobreixen el cos Així, el volum d’una figura plana és zero El volum dels cossos geomètrics simples pot ésser…
teorema de la integral de Cauchy
Matemàtiques
Teorema relatiu a la integració en el camp complex que afirma que, per a tota funció f(z), de variable z complexa, holomorfa en un recinte simplement connex D, i per a qualsevol trajectòria tancada C continguda en D, es verifica: 72185.
Hom pot també enunciar aquest teorema dient que, en les condicions anteriors, la integral de f z entre dos punts de D és independent del camí d’integració elegit, sempre que aquest camí sigui contingut en D Aquest teorema és fonamental per a l’estudi de les funcions de variable complexa i dóna lloc a la teoria de la integració per residus integral Una aplicació immediata és la integral de Cauchy , mitjançant la qual hom pot expressar el valor d’una funció regular f z i de les seves derivades en un punt qualsevol a interior a un contorn al llarg de C , mitjançant les expressions on f a…