Resultats de la cerca
Es mostren 45 resultats
dipiràmide
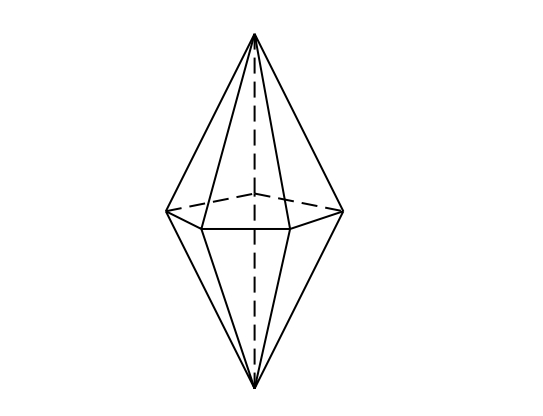
dipiràmide pentagonal
Matemàtiques
Políedre que resulta de soldar, per la base, dues piràmides de bases idèntiques.
S’anomena dipiràmide pentagonal al polídere resultat de soldar dues piràmides pentagonals per les seves bases si les piràmides són regulars, és un deltaedre de deu cares S’anomena dipiràmide triangular al políedre que resulta de soldar dues piràmides triangulars per les seves bases
funció logarítmica complexa
Matemàtiques
Funció f:ℂ-{0}→ℂque resulta d’estendre a ℂla funció exponencial.
És definida per l’assignació z →ln z =ln| z |+ i arg z , on | z | és el mòdul de z i arg z el seu argument És la funció inversa de la funció exponencial complexa e l n z =ln e z = z
recta pròpia
Matemàtiques
Recta que resulta de la intersecció de dos plans no paral·lels.
cubooctàedre
Matemàtiques
Cos que resulta de tallar els vuit angles sòlids d’un cub de manera que en resulta un políedre que té vuit cares que són triangles equilàters i sis cares quadrades.
recta impròpia
Matemàtiques
Recta situada a l’infinit, que resulta de la intersecció de dos plans paral·lels.
octàedre truncat
Matemàtiques
Políedre que resulta de truncar un octàedre regular per quadrats en cadascun dels seus vèrtexs.
Té 6 cares quadrades i 8 d’hexagonals
axioma de la paral·lela
Matemàtiques
Axioma segons el qual per un punt exterior a una recta només es pot traçar una única recta paral·lela a la primera.
L’axioma de la parallela resulta equivalent al cinquè postulat d’Euclides i la seva no-inclusió en el sistema axiomàtic euclidià portà a la descoberta de les geometries no euclidianes
teorema de Bézout
Matemàtiques
Teorema segons el qual el nombre de solucions d’un sistema de n equacions polinòmiques (sense factors en comú per a totes) en n variables, de graus respectius m1,...,mn, és el producte d’aquests: N = m1 · m2...mn (cal tenir en compte les multiplicitats de les solucions i l’eventualitat de solucions infinites).
Com a cas particular, fent n =2, resulta que dues corbes algèbriques planes, d’ordres respectius m 1 i m 2 , tenen m 1 m 2 punts d’intersecció iguals o no
desenvolupament en sèrie
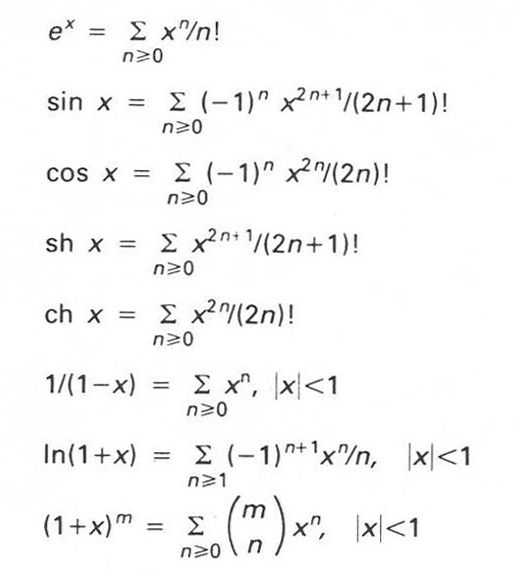
Desenvolupament en sèrie de potències d’algunes funcions
©
Matemàtiques
Expressió d’una funció real, de variable real o complexa,
f(x) ∞
, en termes d’una sèrie de funcions
:
.
La legitimitat d’aquesta igualtat depèn de la convergència de la successió de sumes parcials, en el domini de definició de fx Hom empra, generalment, el desenvolupament en sèrie de potències o sèrie entera, que resulta del teorema de Taylor , i, en el cas de funcions periòdiques, hom empra el desenvolupament en sèrie de Fourier anàlisi de Fourier