Resultats de la cerca
Es mostren 16 resultats
sòlid
Matemàtiques
Porció d’espai limitada per superfícies planes o corbes que dóna lloc a una figura amb tres dimensions (llargària, amplària i profunditat).
angle sòlid
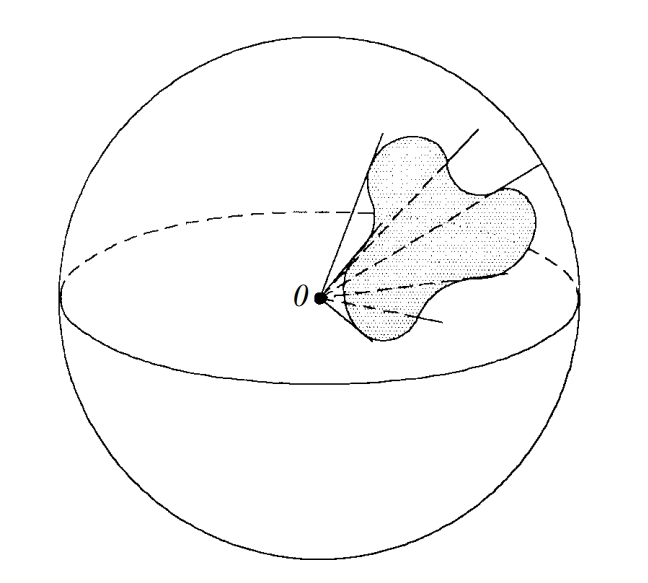
angle sòlid
© Fototeca.cat
Matemàtiques
Espai limitat per la superfície engendrada per una semirecta que, amb origen fix, recorre una línia tancada.
La mesura de l’angle sòlid feta en estereoradians s’obté calculant la superfície de l’esfera, de centre el vèrtex de l’angle sòlid i radi unitat, interceptada per l’angle sòlid
sòlid de revolució
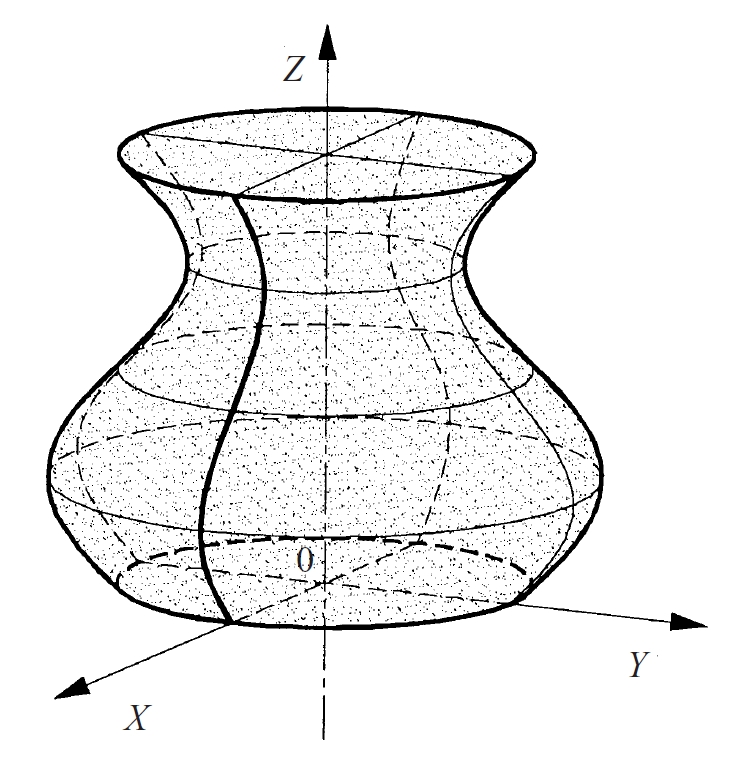
sòlid de revolució
Matemàtiques
Cos limitat per una superfície de revolució, que hom obté per la rotació d’una línia entorn d’un eix.
Així, l’esfera és el sòlid engendrat per un cercle que gira entorn d’un diàmetre el con de revolució és engendrat per una recta o un segment que talla l’eix al voltant del qual gira
estereoradiant
Matemàtiques
Unitat suplementària del Sistema Internacional, que mesura l’angle sòlid.
L’angle sòlid total amb centre en un punt és igual a 4 π estereoradiants
frust
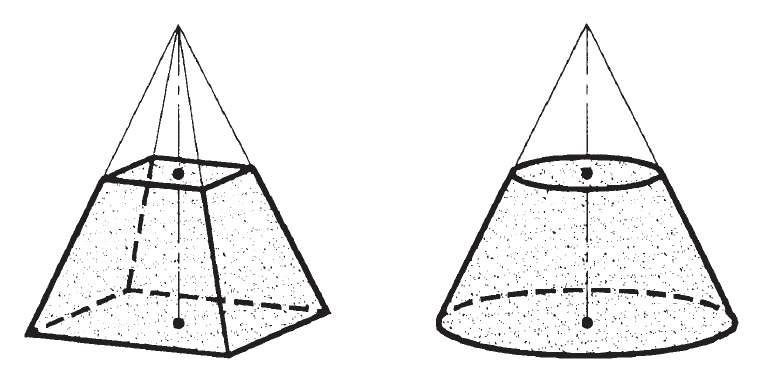
Frusts de piràmide i de con
Matemàtiques
Part d’un sòlid compresa entre dos plans paral·lels o no paral·lels que el tallen.
Quan un dels plans conté la base del sòlid, el frust determinat és anomenat tronc
Louis Poinsot
Matemàtiques
Matemàtic francès.
Fou professor a l’École Polytechnique i s’especialitzà en mecànica Desenvolupà la teoria dels parells i del moviment d’un cos sòlid al voltant d’un punt fix, on introduí el concepte d’inèrcia a la rotació al voltant de certs eixos característics Publicà Éléments de statique 1803 i Nouvelle théorie de la rotation des corps 1832
Francesco Bonaventura Cavalieri
Matemàtiques
Matemàtic i jesuïta italià.
Deixeble de Galileu, des del 1629 fou catedràtic d’astronomia a Bolonya De la seva nombrosa obra es destaquen Geometria indivisibilium continuorum nova quadam ratione promota 1635 i Exercitationes geometricae sex 1647 on establí i perfeccionà la teoria dels indivisibles l’indivisible de Cavalieri equival a l’actual diferencial i exposà la seva gran descoberta, la connexió existent entre la diferenciació i la integració, així com la primera demostració rigorosa del teorema de Papus relatiu al volum d’un sòlid de revolució Resolgué diversos problemes plantejats per Kepler i…
políedre
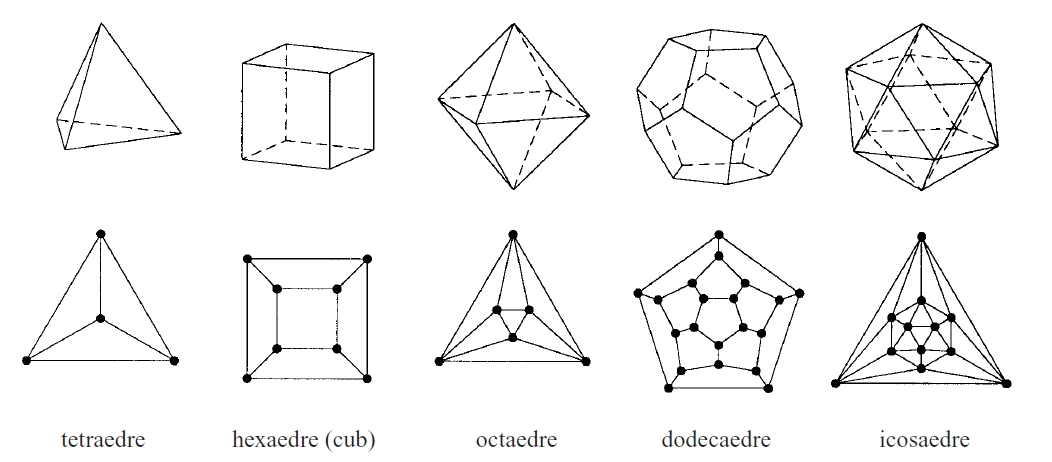
Els cinc políedres regulars i els diagrames de Schlegel associats
© Fototeca.cat
Matemàtiques
Sòlid limitat per quatre o més polígons anomenats cares.
Les interseccions de les cares constitueixen les arestes , i les interseccions de les arestes, els vèrtexs Un políedre és convex si qualsevol secció plana del políedre és un polígon convex Un políedre és còncau si no és convex Un políedre és simple si és topològicament equivalent a una esfera, és a dir, si no té forats Un políedre és regular si té les cares iguals i els angles iguals, essent les cares polígons regulars Des de la Grècia antiga hom sap que existeixen solament cinc políedres regulars el tetràedre regular , l’ hexàedre regular o cub, l’ octàedre regular , el dodecàedre regular i…