Resultats de la cerca
Es mostren 11 resultats
secció
Matemàtiques
Intersecció d’un pla amb una superfície.
Si aquesta és una superfície cònica, hom parla de seccions còniques ellipses, hipèrboles i paràboles, parells de rectes, etc Les seccions produïdes en prismes i cilindres per plans perpendiculars, respectivament, a les arestes laterals i a les generatrius, són anomenades seccions rectes
semblant
Matemàtiques
Dit dels el·lipsoides tals que llurs seccions principals són el·lipses semblants.
hiperboloide
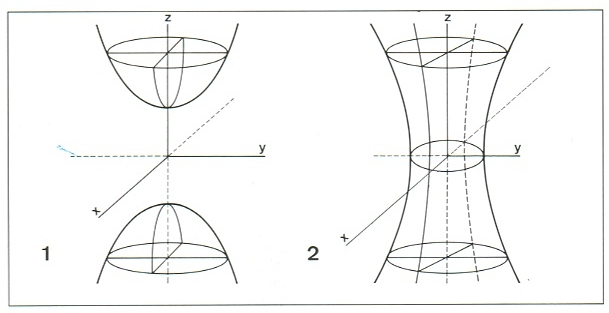
hiperboloide 1, de dues fulles; 2, d'una fulla
Matemàtiques
Quàdrica que, respecte als seus tres eixos de simetria, té per equació (x2/a2) + (y2/b2) - (z2/c2) = ±1.
Entre les seves seccions planes, n'hi ha que són hipèrboles Quan el signe del segon membre és +, l’hiperboloide és anomenat d’una fulla o hiperbòlic quan és -, l’hiperboloide és anomenat de dues fulles o ellíptic Un hiperboloide és anomenat de revolució quan hom el pot considerar generat per la rotació d’una hipèrbola entorn d’un dels seus eixos de simetria
con
Matemàtiques
Superfície reglada generada per totes les rectes (generatrius) que passen per un punt dit vèrtex i per una corba (exterior al punt donat) dita directriu.
La superfície consta de dos fulls units pel vèrtex Es parla de con de revolució si la superfície cònica és engendrada per una recta que passa pel vèrtex i gira al voltant d’una altra recta que també hi passa, la qual és anomenada eix del con Les corbes obtingudes en tallar un con de revolució amb un pla que no passa pel vèrtex reben el nom de seccions còniques o, simplement, còniques Si el pla secant és parallel a una generatriu del con, la cònica rep el nom de paràbola en la resta de casos, el pla secant determina una ellipse o una hipèrbola, segons si el pla talla un full…
Reial Acadèmia de Ciències i Arts de Barcelona

Emblema de la Reial Acadèmia de Ciències i Arts de Barcelona
© Fototeca.cat
Entitats culturals i cíviques
Matemàtiques
Astronomia
Física
Química
Geologia
Biologia
Tecnologia
Institució fundada l’any 1764 amb el nom de Conferència Fisicomatemàtica Experimental amb Francesc Subiràs com a president i Josep Anton Desvalls, marquès de Llupià, com a secretari, limitada inicialment a 16 membres.
Celebrà les primeres reunions a la rebotiga d’una farmàcia i més tard a unes golfes del carrer de la Boqueria, on fou installat un gabinet de màquines d’experimentació El desembre del 1765 es reorganitzà amb el nom de Reial Conferència Física , amb uns nous estatuts pels quals fou designat president el capità general de Catalunya, i amplià el seu abast al conreu de “totes les ciències naturals i l’avenç de les arts útils”, amb nou seccions àlgebra i geometria estàtica i hidroestàtica electricitat magnetisme i òptica pneumàtica i acústica història natural botànica química agricultura El 1770…
cònica
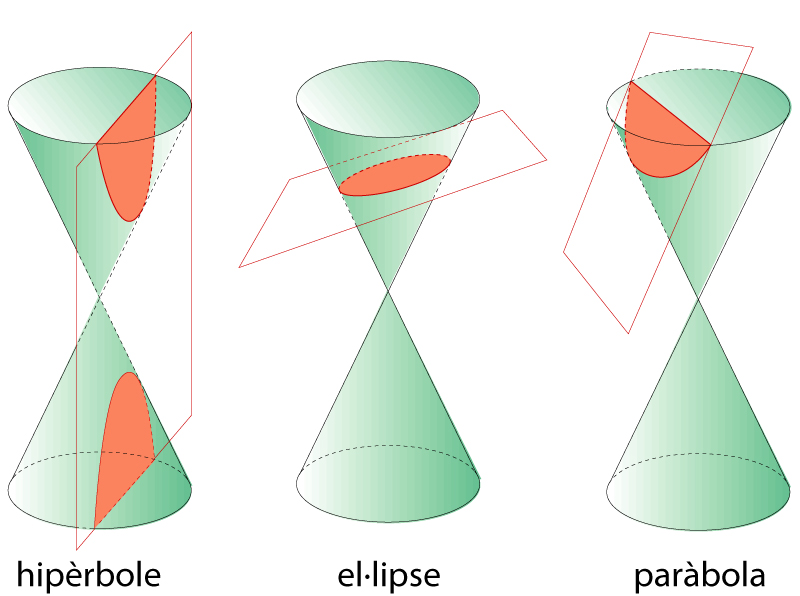
Còniques com a secció de cons
© Fototeca.cat
Matemàtiques
Corba de segon grau en un pla.
El primer estudi conegut sobre còniques és el tractat d’Apolloni de Perge, que les definia com a possibles seccions d’un con Projectivament, hom defineix la cònica com a lloc geomètric dels punts dobles d’una polaritat L’estudi afí de les còniques destaca els següents elements centre , que és el pol de la recta de l’infinit, diàmetre , qualsevol recta que passa pel centre, asímptotes , els diàmetres tangents a la cònica En l’estudi euclidià hom distingeix, a més, els eixos principals, que són una parella de diàmetres perpendiculars i també conjugats respecte a la polaritat…
nombre real
Matemàtiques
Cadascun dels nombres que hom pot obtenir en mesurar magnituds contínues.
Hom obté el conjunt dels nombres reals completant el conjunt dels nombres racionals amb tots els nombres irracionals que poden ésser representats sobre la recta, tals com etc La manera més simple d’introduir teòricament i d’utilitzar en la pràctica els nombres reals és per mitjà de llur expressió decimal Tot nombre real és expressat en forma decimal amb infinites xifres que, en el cas dels nombres irracionals, no es repeteixen periòdicament Això suposa que per a definir un nombre real cal donar una llei que permeti d’obtenir tantes xifres decimals com hom vulgui A la pràctica, però, hom pren…
geometria
Matemàtiques
Part de la matemàtica basada en la intuïció d’espai.
El nom prové de la seva primera aplicació la mesura de la Terra Els diversos apartats en què hom divideix la geometria fan referència a la natura dels objectes d’estudi i al mètode emprat Per a una definició unitària de la geometria elemental, l’any 1872 CF Klein proposà,en el “programa d’Erlangen”,la noció de geometria com a consideració d’un espai el conjunt dels punts i un grup de transformacions d’aquest espai, els invariants del qual serien les nocions de la geometria en qüestió El primer estudi de la geometria fou de caràcter intuïtiu, i consistí en la compilació de fets relatius a…