Resultats de la cerca
Es mostren 37 resultats
categoria
Matemàtiques
Estructura algèbrica composta per una família d’objectes matemàtics i per una família de morfismes entre aquests objectes, tal que satisfà les següents propietats.
per a tot parell X,Y d’objectes de la categoria existeix un conjunt Hom X,Y, anomenat conjunt de morfismes de X en Y, tal que HomX,Y = HomX’,Y’ si i només X=X’ i Y=Y’ i, per a tot triplet X,Y,Z d’objectes de la categoria, existeix una aplicació Hom Y,Z x HomX,Z→HomX,Z, anomenada composició de morfismes, que satisfà l’associativitat i l’existència d’una identitat a cada HomX,X és a dir, existeix un morfisme 1 x tal que per a tot f de HomX,X se satisfà Els objectes d’una categoria no han de formar necessàriament un conjunt, sino una classe així, per exemple, la categoria dels grups G r és…
distància
Matemàtiques
Donat un conjunt E
, aplicació d
: Ex
E →ℝ +
que satisfà els següents axiomes:
o sia, la distància és estrictament positiva, simètrica i compleix la desigualtat triangular.
Tot conjunt E en el qual hi ha definida una distància d és un espai mètric , i d és la mètrica de l’espai Per exemple, en el conjunt dels números reals ℝhom pot considerar d x,y = | x — y |, valor absolut de la diferència x — y , on x,y ∈ℝ
derivació
Matemàtiques
En un anell A, aplicació D:A→A que satisfà les següents propietats: D(a+b) = D(a)+D(b), i D(ab) = (Da)b+a(Db).
En el cos dels reals ℝ, l' aplicació derivada , que assigna a cada funció derivable f la seva derivada f´ , és una derivació
fracció
Matemàtiques
Expressió de la forma n/m, on n i m, anomenats, respectivament, numerador i denominador, són elements d’un domini d’integritat, amb la condició m ≠ 0.
Dues fraccions n/m i n'/m' són iguals si i només si nm' = n'm Hom defineix suma i producte de dues fraccions per les fórmules següents, respectivament n/m + n'/m' = nm' + n'm / mm' i n/m n'/m' = nn'/mm’
teorema de Tales
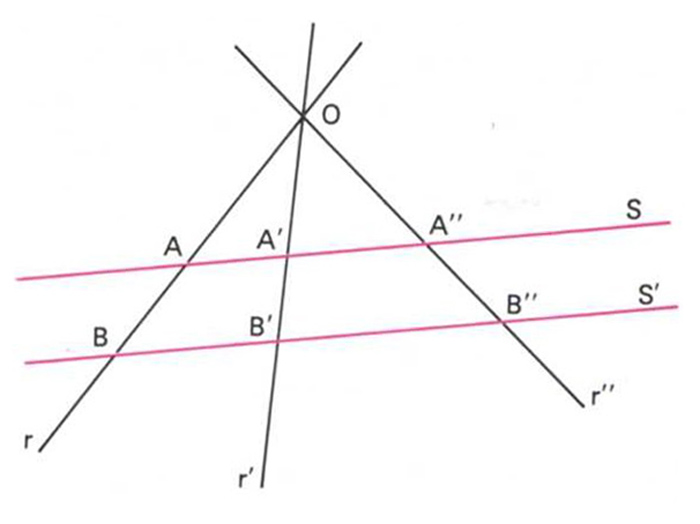
Teorema de Tales
© fototeca.cat
Matemàtiques
Teorema que estableix la proporcionalitat dels segments interceptats per rectes paral·leles sobre un feix de rectes concurrents.
Així, si tres rectes r, r´ i r’ que es tallen en O, són interceptades per les rectes paralleles en S, i en els punts B, B´ i B’ en S´, el teorema de Tales permet d’establir, entre d’altres, les següents relacions
funcions el·líptiques de Jacobi
Matemàtiques
Donats dos reals no nuls, a i a´, tals que a2 + a´2 = 1, funcions inverses de les funcions .
Les funcions inverses de f, g i h es denoten, respectivament, per sn, cn i dn i satisfan les següents propietats cn u + sn snu cnu = 1 dn 2 u + a 2 sn 2 u = 1 cn´ u = -sn u dn u dn'u = - a 2 sn u cn u
àlgebra de Lie
Matemàtiques
Estructura algèbrica consistent en una àlgebra E dotada d’una operació interna, sovint anomenada parèntesi de Lie, (x,y) →[x,y].
Satisfà les següents propietats x,y =0, per a tot x∈E, aquesta segona expressió és la identitat de Jacobi , L’espai euclidià, ℝ 3 , dotat del producte vectorial, té estructura d’àlgebra de Lie Tot grup de Lie té associada una àlgebra de Lie aquestes són, doncs, emprades per a estudiar els grups de Lie
lleis de De Morgan
Lògica
Matemàtiques
En lògica d’enunciats, lleis donades per les equivalències següents: no(P i Q) = (no P) o (no Q), i no(P o Q) = (no P) i (no Q).
En teoria de conjunts, lleis donades per les igualtats i on les barreres indiquen els conjunts complementaris Les lleis de De Morgan se satisfan en tota Boole, àlgebra de
determinant de Vandermonde
Matemàtiques
Determinant que té uns a la primera fila, la segona fila és arbitrària i les files següents són formades per les potències successives dels elements de la segona fila.
Per exemple
postulats d’Euclides
Matemàtiques
Conjunt de cinc principis axiomàtics exposats per Euclides en l’obra Elements, en els quals fonamentà la seva geometria.
Són els següents donats dos punts qualssevol, hom pot traçar una recta que els uneix tota línia recta finita es pot prolongar indefinidament donat un punt qualsevol, hom pot traçar una circumferència amb radi arbitrari i centre en el punt esmentat tots els angles rectes són iguals entre ells i, finalment, donada una recta i un punt exterior, hom només pot traçar per aquest una recta parallela a la recta donada