Resultats de la cerca
Es mostren 31 resultats
principi de Cantor
Matemàtiques
Principi segons el qual, en la recta real, tota successió d’intervals tancats tals que cada un és contingut en l’anterior i les longituds dels quals tendeixen a zero, defineix un nombre real.
Si a n ,b n és la successió d’intervals, essent a n una successió no decreixent i b n una successió no creixent tals que la diferència b n -a n es mantingui sempre positiva, però tendint a zero quan n tendeix a infinit, el teorema de Cantor afirma que hi ha un únic nombre real x tal que x és contingut en qualsevol dels intervals a n ,b n
segment esfèric

Dos segments esfèrics, de dues bases i d’una base, respectivament
© Fototeca.cat
Matemàtiques
Part de l’espai limitada per un pla secant a una esfera i la superfície d’aquesta.
inversió
Matemàtiques
Transformació geomètrica del pla o de l’espai que, donat un punt O
, anomenat centre d’inversió
, i un nombre k
, anomenat potència
, fa correspondre a cada punt P
un altre punt P´
.
De manera que O, P i P' són alineats, i els segments compleixen la relació La inversió és una transformació isogonal
mitjana
Matemàtiques
En un triangle, segment que va d’un vèrtex al centre del costat oposat.
Tot triangle té tres mitjanes, que es tallen en un únic punt, anomenat baricentre El baricentre divideix cada mitjana en dos segments, el segment baricentre-vèrtex essent el doble de llarg que l’altre
polígon
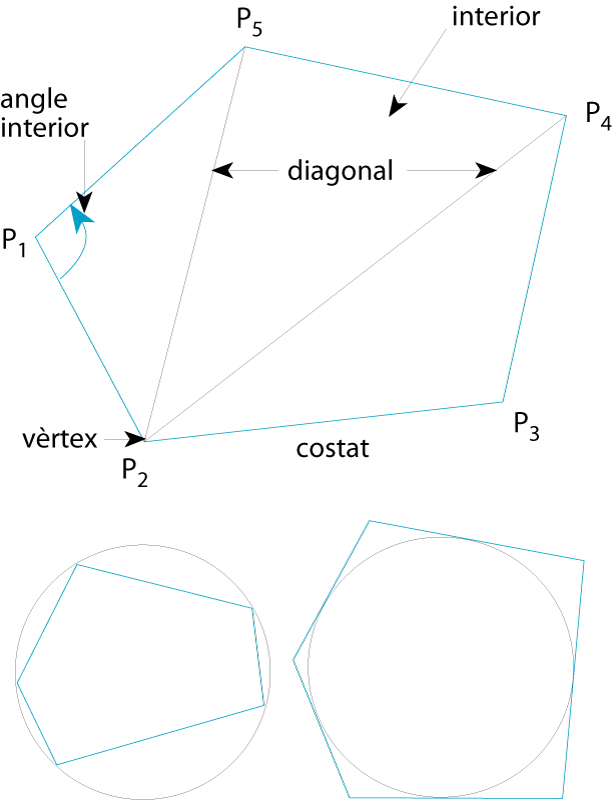
Elements d’un polígon (dalt); polígon inscrit en un cercle (baix esquerre); polígon circumscrit a un cercle (baix dreta)
© Fototeca.cat
Matemàtiques
Figura plana i tancada formada per segments rectes.
P 1 P 2 , P 2 P 3 , P n - 1 P n , i P n P 1 , són anomenats costats del polígon, essent els punts P 1 , P 2 , , P n , amb n ≥3, els anomenats vèrtexs del polígon Una diagonal del polígon és el segment recte que uneix dos vèrtexs no correlatius La porció de pla que és envoltada pels costats constitueix l' interior del polígon Els angles determinats per cada parell de costats adjacents, i que són a l’interior, són dits angles interiors del polígon Un polígon és convex si cada angle interior és menor o igual a 180° Un polígon és còncau si no és convex, és a dir, si almenys existeix un angle…
homotècia
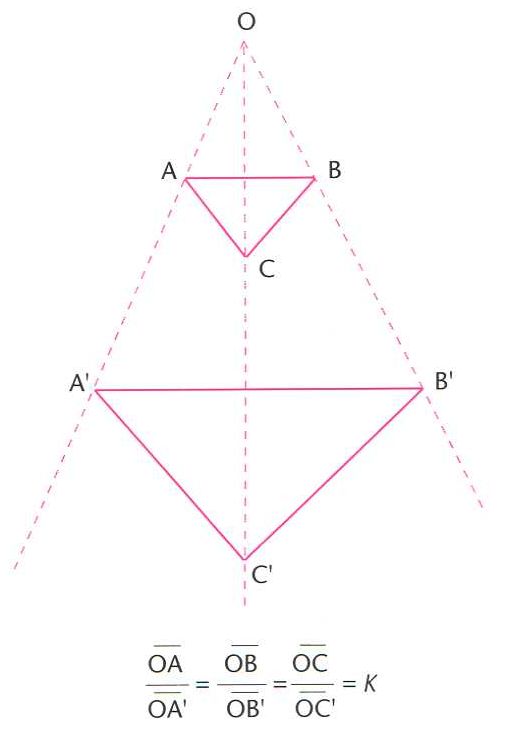
Homotècia, transformació homotètica d’un triangle ABC (O, centre de l’homotècia; k, raó d’homotècia)
© Fototeca.cat
Matemàtiques
Transformació geomètrica del pla o de l’espai que compleix aquestes dues condicions.
Qualsevol punt A i la seva imatge A' són alineats amb un punt fix O anomenat centre d’homotècia , i els segments compleixen la relació k essent, per a cada homotècia, una constant real anomenada raó de l’homotècia Les homotècies transformen rectes en rectes, circumferències en circumferències i conserven els angles
regle de càlcul

Regle de càlcul
(CC0)
Construcció i obres públiques
Matemàtiques
Petit instrument portàtil de fusta, metall, plàstic, etc. que permetia fer càlculs numèrics d’una manera ràpida i amb una certa aproximació raonable.
Consisteix en un regle proveït de diverses escales graduades, que duu, a més, un petit regle també graduat, desplaçable respecte al regle principal mitjançant unes ranures i uns encaixos adequats, i un cursor transparent, també desplaçable, proveït d’una o més ratlles verticals molt fines Totes les escales són logarítmiques, llevat d’alguna d’especial El principi en què es basa el regle de càlcul és la teoria dels logaritmes, de manera que per a multiplicar dos nombres, de fet hom suma dos segments graduats logarítmicament, i la divisió, anàlogament, consisteix a fer la diferència dels dos…
nombre racional
Matemàtiques
Conjunt de fraccions equivalents que representen una mateixa quantitat, entera o no.
Dues fraccions a / b , c / d són equivalents o iguals si, i només si, els parells de nombres enters que les constitueixen compleixen la relació ad = bc Cada classe de fraccions equivalents en aquesta relació d’equivalència és un nombre racional Si la fracció que defineix un nombre racional té numerador múltiple del denominador, és a dir, a = kb k ∈ℤ, la fracció a / b és equivalent a k/ 1, que hom acostuma a escriure en la forma k/ 1 = k En aquest sentit hom pot dir que els nombres enters són un subconjunt dels racionals Entre els nombres racionals hom pot definir les operacions d’addició i…
trigonometria

1, circumferència de referència per a la definició de les raons trigonomètriques; 2, representació gràfica de les línies trigonomètriques; 3, símbols emprats en la resuloció de triangles
© fototeca.cat
Matemàtiques
Part de la matemàtica inicialment dedicada a l’estudi de les relacions entre les amplituds dels angles i les longituds dels segments que llurs costats determinen en les rectes que tallen.
La trigonometria es basa en les propietats de les anomenades raons trigonomètriques , que són definides a partir d’un punt P x,y d’una circumferència de centre O i per l’angle α que forma el radi r = OP amb l’eix OX , mitjançant els sis quocients següents sin α = y/r sinus cos α = x/r cosinus tg α = y/x tangent cotg α x/y cotangent sec α = r/x secant cosec α = r/y cosecant Quan el punt P és a una distància r = 1 de l’origen O , el valor absolut d’aquestes raons és representat per la longitud de certs segments anomenats línies trigonomètriques , respectivament, fàcils de traçar A partir de…
August Ferdinand Möbius
Astronomia
Matemàtiques
Matemàtic i astrònom alemany.
La seva obra Der barycentrische Calcül 1827, fonamental per al desenvolupament de la geometria projectiva, aportà nombroses innovacions orientació sistemàtica dels segments, àrees i volums, concepte de raó anharmònica, noció general de transformació homogràfica, etc Estudià les transformacions circulars sobre el pla en la seva obra Theorie der Kreisverwandschaft 1855 Donà el primer exemple de superfície unilateral amb la coneguda banda o cinta de Möbius La seva obra completa Gesammelte Werke fou publicada en quatre volums a Leipzig durant els anys 1885-87