Resultats de la cerca
Es mostren 64 resultats
segon
Matemàtiques
Unitat de mesura d’angles.
Segons que la divisió de la circumferència sigui la sexagesimal o la centesimal, el segon corresponent és anomenat sexagesimal símbol ' o centesimal símbol ''
teoremes de Guldin
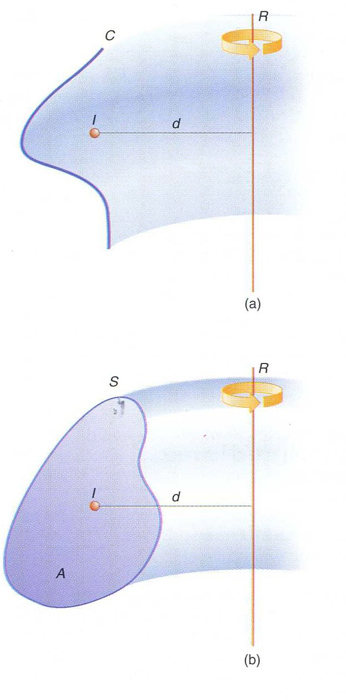
teoremes de Guldin: (a) primer teorema; (b) segon teorema
© fototeca.cat
Matemàtiques
Teoremes que relacionen el centre de massa d’una corba o d’una superfície amb l’àrea o el volum, respectivament, que generen en girar al voltant d’un eix.
Segons el primer teorema de Guldin , donada una corba plana C , de longitud l , que gira al voltant d’una recta R del seu pla, la qual no talla, l’àrea A de la superfície de revolució que genera és A = 2π dl , on d és la distància des del centre de massa I de la corba a la recta R en el cas purament geomètric, el centre de massa és calculat assignant la mateixa “massa” a tots els punts de la corba matemàtica en el cas físic, el centre de massa és el del sistema de masses puntuals de la corba material El segon teorema de Guldin afirma que, donada una superfície plana S , d’àrea A…
quadràtic | quadràtica
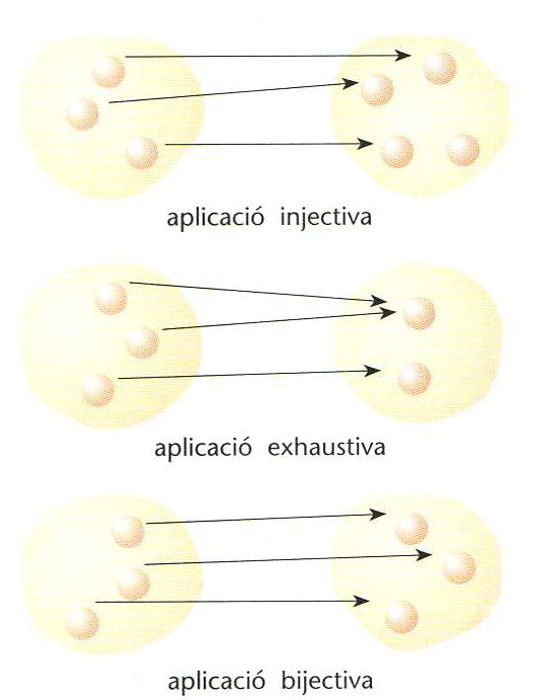
aplicació
fototeca.cat
©
Matemàtiques
correspondència
entre dos conjunts en què tot element del primer conjunt (o original) té una imatge i una de sola en el segon conjunt.
Si elements diferents tenen imatges diferents, l’aplicació és dita injectiva si tot element del segon conjunt és imatge d’un element almenys del primer, l’aplicació és exhaustiva una aplicació que sigui alhora injectiva i exhaustiva és dita bijectiva o unívoca
cònica
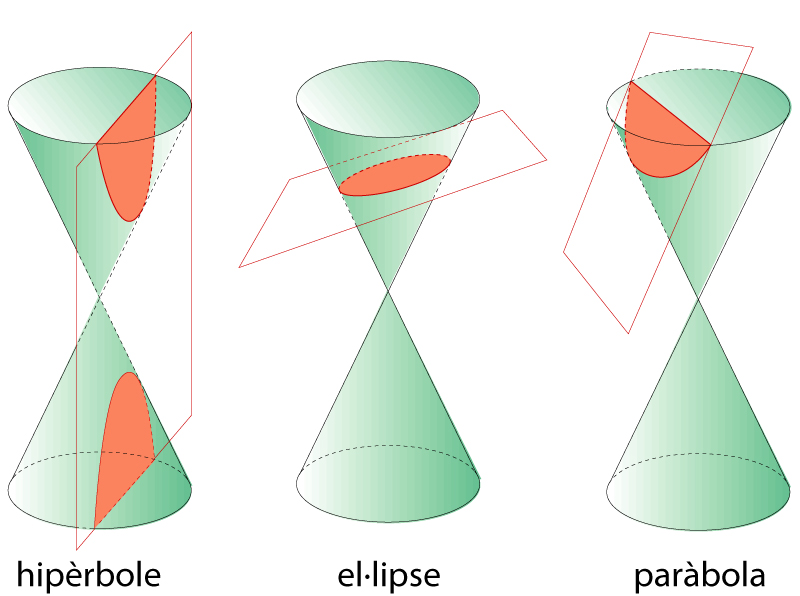
Còniques com a secció de cons
© Fototeca.cat
Matemàtiques
Corba de segon grau en un pla.
El primer estudi conegut sobre còniques és el tractat d’Apolloni de Perge, que les definia com a possibles seccions d’un con Projectivament, hom defineix la cònica com a lloc geomètric dels punts dobles d’una polaritat L’estudi afí de les còniques destaca els següents elements centre , que és el pol de la recta de l’infinit, diàmetre , qualsevol recta que passa pel centre, asímptotes , els diàmetres tangents a la cònica En l’estudi euclidià hom distingeix, a més, els eixos principals, que són una parella de diàmetres perpendiculars i també conjugats respecte a la polaritat induïda per la…
Pío Beltrán Villagrasa
Diplomàtica i altres branques
Numismàtica i sigil·lografia
Matemàtiques
Epigrafista i numismàtic, professor de matemàtiques a l’institut de segon ensenyament a València.
Destacà pels estudis de numismàtica hispànica, sobretot antiga i medieval, i d’epigrafia ibèrica En aquest camp fou des dels anys cinquanta un dels capdavanters de la teoria del bascoiberisme Treballà també sobre inscripcions romanes de Tarragona i de Sagunt Entre els seus nombrosos estudis cal destacar Sobre un interesante vaso escrito de San Miguel de Liria, Los textos ibéricos de Liria i El plomo escrito de la Bastida de Les Alcuses Mogente
autònom | autònoma
Matemàtiques
Dit de les equacions diferencials ordinàries de segon ordre que són reductibles a una de primer ordre.
equació quadràtica
Matemàtiques
Equació de segon grau ax2 + bx + c = 0, o, en forma reduïda, x2 + px + q = 0.
Una equació quadràtica pura és la de la forma ax 2 + b = 0 En ax 2 + bx + c = 0, la fórmula de la solució és la quantitat b 2 - 4ac és anomenada discriminant
aplicació exhaustiva
Matemàtiques
Aplicació entre dos conjunts en què tot element del segon conjunt és imatge d’un element, almenys, del primer.
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- Pàgina següent
- Última pàgina