Resultats de la cerca
Es mostren 27 resultats
axiomàtica
Filosofia
Matemàtiques
Conjunt d’axiomes no contradictoris i independents que es formulen per a poder desenvolupar una teoria d’una manera deductiva lògicament correcta.
La matèria que es presta més a ésser tractada en forma axiomàtica és la matemàtica, bé que el mètode és aplicable al desenvolupament teòric d’altres ciències física, economia, estadística, etc Cada una de les proposicions admeses com a base de l’estudi axiomàtic d’una teoria és anomenada axioma o postulat aquests dos mots, en matemàtiques, són considerats sinònims Un sistema de postulats és un conjunt de proposicions breus que tradueixen les veritats fonamentals de la teoria a la qual serveixen de base És desitjable que els postulats d’un sistema siguin simples , és a dir, que…
gràfic | gràfica
Matemàtiques
Subconjunt del producte cartesià A × B de dos subconjunts; es tracta doncs, d’una colla de parelles d’elements (a, b), on a ∈A i b ∈B.
En el cas que A i B siguin, respectivament, el domini de definició i la imatge d’una funció, el gràfic corresponent és anomenat també gràfica funcional o corba associada a la funció
desigualtat de Schwarz
Matemàtiques
Desigualtat enunciada per H.A. Schwarz, que es compleix en tot espai vectorial E dotat d’un producte escalar <, >, expressada per |<x,y>|2≤<x,x> <y,y>.
La igualtat es dóna només en el cas que x,y siguin linealment dependents y = a x , essent a un nombre Aquesta desigualtat és fonamental en l’estudi dels espais de Hilbert, estructures bàsiques de l’anàlisi funcional
linealitzar
Matemàtiques
Simplificar un problema substituint les expressions exactes per unes altres expressions aproximades que siguin polinomis de primer grau.
Hermann Bondi
Astronomia
Matemàtiques
Matemàtic i cosmòleg anglès d’origen austríac.
Amb Thomas Gold i Fred Hoyle, és l’autor de la teoria cosmològica dita de l’estat estacionari Steady-State de l’univers 1948, que parteix del “principi cosmològic perfecte” segons el qual l’univers presenta el mateix aspecte qualssevol que siguin el lloc i l’instant de l’observació cosmologia La seva obra més important és Cosmologia 1952
corbes de Lissajous
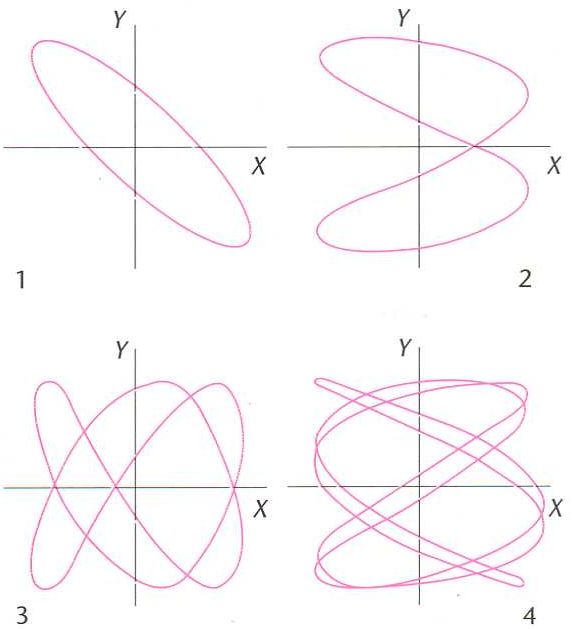
Corbes de Lissajous la relació entre les pulsacions wx i wy dels dos moviments corresponents.
© Fototeca.cat
Matemàtiques
Corbes que apareixen en la composició de dos moviments vibratoris harmònics perpendiculars entre ells.
Hom obté corbes molt diverses, en general obertes, però, si la relació entre els períodes dels dos moviments és racional, la corba obtinguda és tancada i el moviment resultant és periòdic si els dos períodes són iguals, la corba resultant és una circumferència o una ellipse Hom les pot reproduir fàcilment en un oscilloscopi fent que les tensions horitzontal i vertical siguin sinusoidals
conjunt ordenat
Matemàtiques
Conjunt X
proveït d’una relació d’ordre ≤.
Si la relació d’ordre és parcial, el conjunt OOO X ,≤OOO és parcialment ordenat i, si és total, és totalment ordenat Una relació d’ordre és parcial si compleix les propietats reflexiva x ≤ x , transitiva si x ≤ y i y ≤ z , aleshores x ≤ z i antisimètrica si x ≤ y i y ≤ x , aleshores x = y I és total quan és parcial i, a més, tota parella d’elements és comparable qualssevol que siguin x , y , x ≤ y o y ≤ x
mínim relatiu
Matemàtiques
Valor que pren una funció f(x) en un punt x=a quan aquest valor és menor que els valors de f(x) en els punts immediatament anteriors i posteriors al punt a.
És anomenat també mínim local , i en el cas particular que existeixen les derivades successives de f x es compleix que en el punt a la primera derivada f ' a és nulla i la segona, f ' a , normalment és positiva En el cas, però, que tant f ' a com f ' a siguin nulles, la condició que f x tingui un mínim en el punt a és que la primera derivada de f x no nulla en el dit punt sigui d’ordre parell i positiva Aquestes són les condicions que hom aplica per a trobar els mínims d’una funció
màxim relatiu
Matemàtiques
Valor que pren una funció f(x) en un punt x=a quan aquest valor és més gran que els valors de f(x) en els punts immediatament anteriors i posteriors al punt a.
És anomenat també màxim local, i, en el cas particular que existeixin les derivades successives de f x , es compleix que en el punt a la primera derivada f' a és nulla i la segona f' a normalment és negativa En el cas, però, que tant f' a com f' a siguin nulles, la condició que f x tingui un màxim en el punt a és que la primera derivada de f x no nulla en el dit punt sigui d’ordre parell i negativa Aquestes són les condicions que hom aplica per a trobar els màxims d’una funció
simulació
Matemàtiques
Tècnica emprada en investigació operativa.
Consisteix a construir un model simbòlic d’un sistema o d’un procés complex, de manera que els seus elements siguin representats mitjançant els processos lògics i aritmètics que hom pot executar amb un programa d’ordinador, a fi d’estudiar el comportament del sistema i mesurar-ne les propietats dinàmiques, a base d’obtenir les característiques estadístiques del dit comportament Això permet d’avaluar i comparar diferents estratègies d’operació del sistema, sense que aquest existeixi realment Les aplicacions més conegudes d’aquesta tècnica han estat fetes en l’estudi de xarxes d’…