Resultats de la cerca
Es mostren 29 resultats
simetria
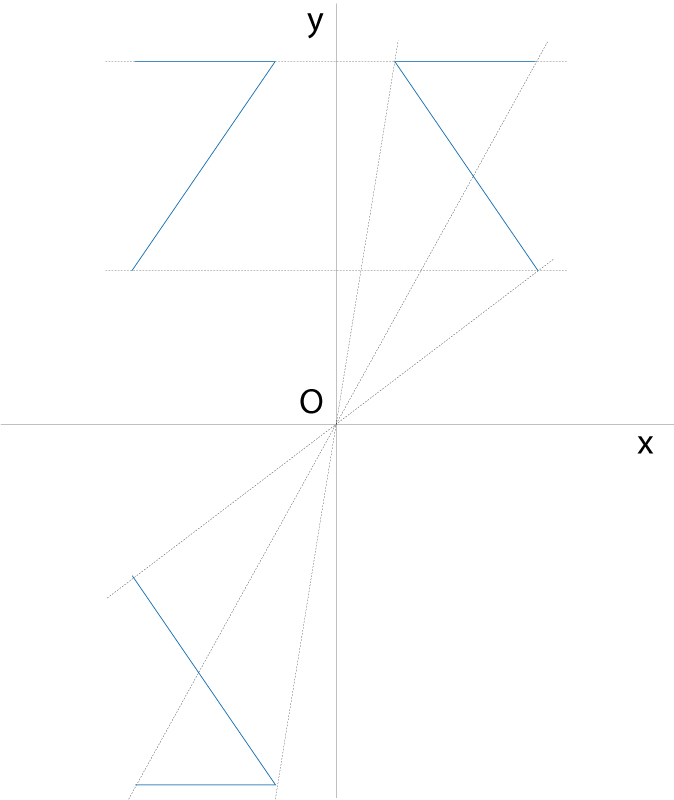
Dues figures obtingudes per simetria axial i central
© Fototeca.cat
Matemàtiques
Configuració d’un objecte que és invariant per a determinats moviments geomètrics.
Dins el concepte de simetria hom estudia modernament tots el moviments geomètrics del pla i de l’espai Una simetria axial és la transformació que per a tot punt P n'assigna un altre P' , de manera que la recta PP' és perpendicular a una recta donada dita eix de simetria i les distàncies de P a l’eix i de P' a l’eix són iguals Una simetria especular és la transformació que per a tot punt P n'assigna un altre P' , de manera que la recta PP' és perpendicular a un pla donat dit pla de simetria i les distàncies de P al pla i de P'…
grup de simetria

Els disset grups de simetria del pla
© Fototeca.cat
Matemàtiques
Grup format per totes les isometries que deixen invariant una certa figura.
eix de simetria
Física
Matemàtiques
Recta al voltant de la qual les parts d’un cos o sistema gaudeixen de simetria.
configuració simètrica
Matemàtiques
Configuració geomètrica tal que per a tot punt A de la configuració hi ha un altre punt B, anomenat simètric, els quals equidisten respecte a un element prefixat, que pot ésser un punt (centre de simetria), una línia (eix de simetria) o un pla (pla de simetria).
En aquests tres casos hom parla respectivament de simetria central, axial o especular simetria Aplicant simetries a una configuració qualsevol hom obté una nova configuració composta simètrica
hiperboloide
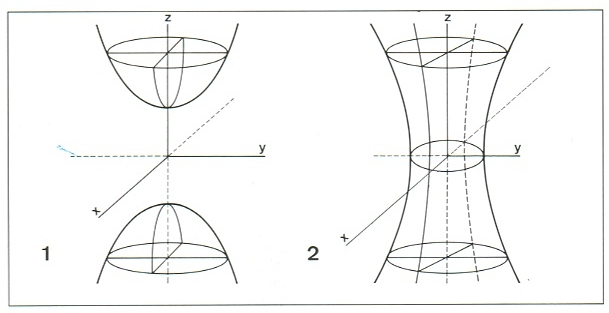
hiperboloide 1, de dues fulles; 2, d'una fulla
Matemàtiques
Quàdrica que, respecte als seus tres eixos de simetria, té per equació (x2/a2) + (y2/b2) - (z2/c2) = ±1.
Entre les seves seccions planes, n'hi ha que són hipèrboles Quan el signe del segon membre és +, l’hiperboloide és anomenat d’una fulla o hiperbòlic quan és -, l’hiperboloide és anomenat de dues fulles o ellíptic Un hiperboloide és anomenat de revolució quan hom el pot considerar generat per la rotació d’una hipèrbola entorn d’un dels seus eixos de simetria
simètric | simètrica
reflexió
Matemàtiques
Simetria respecte a un pla (simetria especular) o a una recta.
paràbola
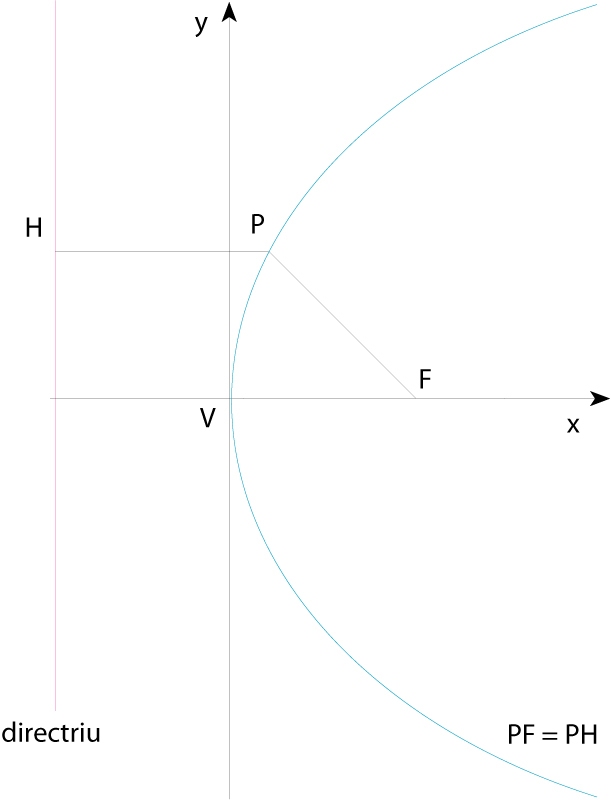
Paràbola (V vèrtex, F focus, P punt qualsevol de la paràbola)
© Fototeca.cat
Matemàtiques
Corba oberta, intersecció d’una superfície cònica amb un pla paral·lel a una de les generatrius.
Constitueix el lloc geomètric dels punts del pla que equidisten d’un punt el focus de la paràbola i d’una recta que no conté el punt la directriu de la paràbola Té un eix de simetria que és la recta perpendicular que passa pel focus i que talla la paràbola en un punt anomenat vèrtex Referida a l’eix de simetria i a la seva perpendicular pel vèrtex, l’equació de la paràbola és y 2 =2 px , on p és la distància entre focus i directriu, anomenada paràmetre de la paràbola Hom pot demostrar que la gràfica de tota funció polinòmica de segon grau y= ax 2 + bx+ c és una…
punt fix
Matemàtiques
En una aplicació f, punt x que verifica la condició f(x) = x.
També és anomenat punt doble Per exemple, el centre de simetria és un punt doble en la simetria central Brouwer ha demostrat l’anomenat teorema del punt fix , segons el qual tota aplicació contínua en una esfera n -dimensional amb ng 2 té un punt fix El teorema té com a conseqüència que la major part de les deformacions físiques tinguin punts fixos
paraboloide hiperbòlic
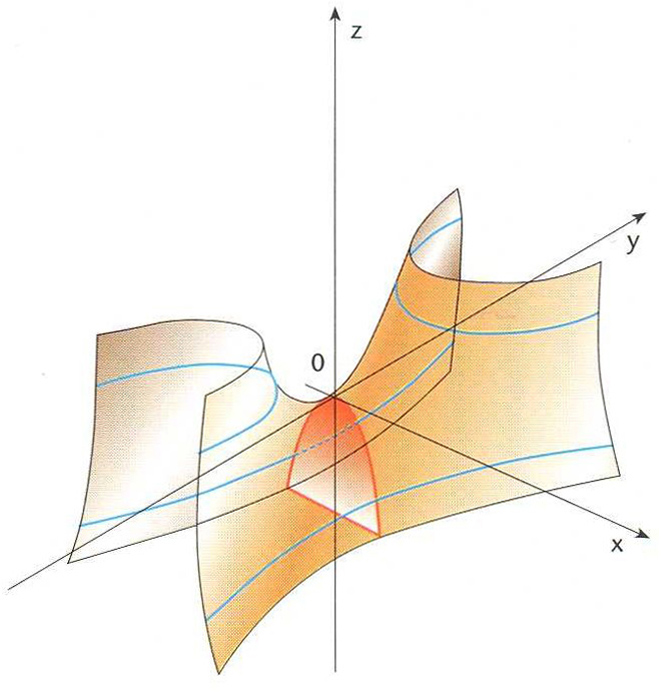
Paraboloide hiperbòlic on hi ha traçada una paràbola i dues hipèrboles
© Fototeca.cat
Matemàtiques
Paraboloide d’equació
x 2
/a 2
—
y 2
/b 2
= 2 z
, on a
i b
són constants.
La seva intersecció amb un pla que contingui l’eix de simetria és una paràbola i la intersecció amb un pla perpendicular a l’anterior és una hipèrbola