Resultats de la cerca
Es mostren 51 resultats
sistema de coordenades
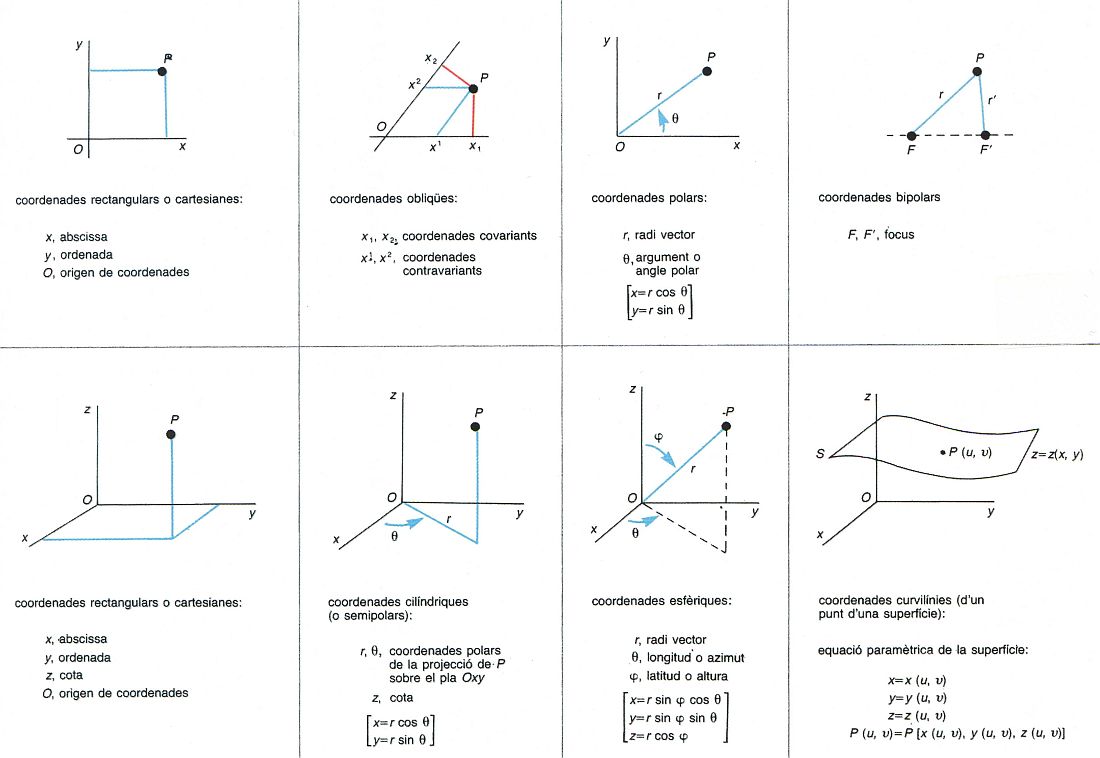
Sistemes de coordenades matemàtiques: coordenades d’un punt del pla (superior) i d’un punt de l’espai (inferior)
©
Matemàtiques
En un cert domini X, conjunt de funcions tal, que els valors en un punt el determinen, de manera que mitjançant un sistema de coordenades cada punt és definit per un conjunt de nombres, que són les coordenades del punt.
Segons els casos les funcions d’un sistema han de complir certes condicions Així, en el pla, un sistema de coordenades lineal consisteix en dues funcions lineals independents Els eixos del sistema són les rectes que corresponen al valor zero de cadascuna de les funcions La intersecció dels dos eixos és l' origen de coordenades Si els eixos són perpendiculars, el sistema és rectangular i les coordenades són rectangulars o cartesianes Si els eixos són oblics, les coordenades són obliqües o rectilínies obliqües En aquest cas, hom pot considerar les coordenades covariants o contravariants , que…
Aleksandr Mikhajlovič Ljapunov
Matemàtiques
Matemàtic i enginyer rus.
Professor a Kharkiv i a Peterburg, féu importants estudis matemàtics sobre les equacions diferencials, el càlcul de probabilitats, etc i mecànics sobre sistemes en equilibri o en moviment, sobre hidrodinàmica, potencials, etc Desenvolupà especialment una teoria general de l’estabilitat i de la regulació de sistemes no lineals
teorema de Rouché-Frobenius
Matemàtiques
Teorema que permet la classificació dels sistemes lineals d’equacions.
Donat un sistema no homogeni de m equacions lineals amb n incògnites, escrit en forma matricial A x = b , b ≠ 0 , on A és la matriu de coeficients del sistema, b la columna dels termes independents i x la columna de les incògnites, el sistema és compatible és a dir, que té solucions si el rang de A és igual al rang de la matriu ampliada A , b matriu Si aquest rang és igual al nombre d’incògnites, aleshores es tracta d’un sistema compatible determinat o sia, amb solució única, però si el rang és menor que el nombre d’incògnites, es tracta d’un sistema compatible…
Carles Simó i Torres

Carles Simó i Torres
© Universitat de Barcelona
Matemàtiques
Matemàtic.
Llicenciat en enginyeria industrial per la Universitat Politècnica de Catalunya i en matemàtiques per la Universitat de Barcelona, on es doctorà l’any 1974, des del 1975 és catedràtic de matemàtica aplicada i anàlisi de la UB Autor de més de 200 articles, ha estudiat les propietats generals dels sistemes dinàmics, els sistemes hamiltonians i dissipatius, la mecànica celeste, l'astrodinàmica i l'anàlisi numèrica, l’anàlisi i el disseny d’òrbites de ginys espacials i els sistemes dinàmics assistits per ordinador Ha combinat mètodes diversos analític,…
sistema d’equacions lineals
Matemàtiques
Conjunt d’equacions lineals de les quals interessen les solucions comunes.
Un sistema d’aquest tipus és anomenat compatible si admet solució, i incompatible en el cas contrari Un sistema compatible és determinat si la solució és única, i indeterminat si, per contra, hi ha infinites solucions Els sistemes d’equacions lineals són anomenats no homogenis si els termes independents b 1 , b m no són tots nuls, i homogenis en el cas contrari La regla de Cramer permet, mitjançant l’ús dels determinants, de resoldre els sistemes de 3 equacions amb 3 incògnites té solució on és el determinant del sistema, que ha d’ésser no nul
simulació
Matemàtiques
Tècnica emprada en investigació operativa.
Consisteix a construir un model simbòlic d’un sistema o d’un procés complex, de manera que els seus elements siguin representats mitjançant els processos lògics i aritmètics que hom pot executar amb un programa d’ordinador, a fi d’estudiar el comportament del sistema i mesurar-ne les propietats dinàmiques, a base d’obtenir les característiques estadístiques del dit comportament Això permet d’avaluar i comparar diferents estratègies d’operació del sistema, sense que aquest existeixi realment Les aplicacions més conegudes d’aquesta tècnica han estat fetes en l’estudi de xarxes d’…
axiomatització
Filosofia
Matemàtiques
Utilització, per part d’una ciència, d’una estructura formalitzada o sistema purament abstracte i formal, que parteix d’uns axiomes o postulats i s’expressa en un simbolisme el més precís possible (axiomàtica).
L’axiomatització té la seva aplicació sobretot en lògica i matemàtiques L’axiomatització d’una ciència pot ésser feta de diverses maneres, puix que per a cada una hi ha diversos sistemes d’axiomes equivalents L’elecció d’un sistema d’axiomes o altre depèn del fi de base crítica dels fonaments, exposició didàctica, aplicacions tècniques, etc Una de les tendències de la lògica actual és de descobrir els mètodes més precisos d’axiomatització i una teoria completa dels símbols lògics per poder fomalitzar tant com sigui possible tots els sistemes L’axiomatització d’una…
Lotfi A. Zadeh

Lofti A. Zadeh
© Franklin Institute Awards
Matemàtiques
Matemàtic nord-americà d’origen azerbaidjanès.
Estudià a Teheran enginyeria elèctrica El 1944 s’installà als EUA i estudià al Massachusetts Institute of Technology i a la Columbia University, on es doctorà el 1949 Fou professor d’aquesta universitat i, posteriorment, de la University of California, on dirigí el Berkeley Initiative for Soft Computing Feu notables contribucions a la teoria dels sistemes, exposades en l’obra Linear System Theory 1963, amb CA Desoer El 1964 introduí el mètode anomenat dels conjunts difusos , per tal de tractar d’una manera matematicooperativa la vaguetat associada a la parla habitual, teoria que …
rampa
Electrònica i informàtica
Matemàtiques
Funció que creix linealment amb el temps des de zero fins a un valor determinat, d’acord per tant amb l’expressió f(t) = kt
.
És una funció emprada sobretot en anàlisi transitòria de circuits elèctrics i sistemes complexos
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- Pàgina següent
- Última pàgina