Resultats de la cerca
Es mostren 22 resultats
tribu
Matemàtiques
Família de subconjunts d’un conjunt Ω.
Presenta tres propietats per a tot element de la família, el seu complementari també hi pertany per a tota successió A n n ∈ℕ d’elements de la família, ∪ A n també hi pertany i el conjunt Ω pertany a la família La tribu generada per una família de subconjunts M és la intersecció de totes les tribus que contenen M i resulta la mínima tribu que conté M Així, donat un conjunt Ω, el conjunt R Ω de les parts de Ω és una tribu a més, és la més gran de totes les tribus de conjunts de Ω La tribu de Borel o dels borelians de ℝ és la generada per tots els intervals oberts de ℝ
uniformitat
Matemàtiques
Família F de subconjunts d’un producte cartesià T × T
.
Compleix x,x pertany a qualsevol element de F , per a tot x si V és de F, V - 1 = { x,y | y,x és de V} és també de F i per a tot V de F existeix un altre W tal que WW = { x,z | existeix y en T i x,y ∈ W , y,z ∈ W} és un subconjunt de V Tota uniformitat dóna lloc a un espai topològic i aquest és metritzable la seva topologia prové d’una distància si és de Hausdorff i la uniformitat té una base numerable Per exemple, si T és un espai mètric, amb distància d , el conjunt de subconjunts de T × T , U ∈ = { x,y | d x,y πε} és una uniformitat La parella T,F , on T és…
recobriment d’un conjunt
Matemàtiques
Família de subconjunts d’un conjunt donat tal, que la seva reunió conté el conjunt en qüestió, que és aleshores anomenat conjunt recobert
.
Les particions són un tipus particular de recobriment El recobriment és finit si és format per un nombre finit de subconjunts
subconjunt
Matemàtiques
Qualsevol conjunt contingut en un altre conjunt, és a dir, que tot element d’aquest ho és d’un altre.
Un subconjunt és una part d’un conjunt Si A és un subconjunt de B, hom ho representa així A⊆B La negació de A⊆B és representada per A⊄B El símbol ⊆és anomenat d’inclusió Tot conjunt admet els subconjunts trivials ell mateix i el conjunt buit ø La collecció de subconjunts d’un conjunt donat A forma un altre conjunt, dit conjunt de les parts de A , que hom representa per P A, i, per tant, PA = {BB⊆A} Si té n elements, PA en té 2 n
component connexa
Matemàtiques
En un espai topològic, subespai connex
.
Sigui un punt x d’un espai topològic , és la unió de tots els subconjunts connexos de X que contenen x Les components connexes són sempre tancades i, si són diferents són disjuntives
combinació
Matemàtiques
Configuració on hom només té en compte la distinció entre els elements agrupats i no l’ordre en què són presos.
Hom anomena combinació d’ordre n , formada a partir d’un conjunt de m elements 0 ≤ n≤ m, qualsevol dels subconjunts formats en considerar n elements diferents entre els m que integren el conjunt donat, sense tenir-ne en compte l’ordre hom considera, doncs, que dues combinacions són distintes quan algun de llurs elements és diferent El nombre de combinacions d’ordre n , formades a partir d’un conjunt amb m elements, és donat per l’expressió on V n m indica el nombre de variacions, i P n el de permutacions Hom representa sovint C n m per n m , parlant, en aquest, cas, de nombres…
àlgebra de Boole
Matemàtiques
Conjunt A en què s’han definit una operació unitària ¬ i dues operacions binàries ∨ i ∧, i amb dos elements distingits 0 i 1, de manera que per tot x, y, z de A se satisfan les següents propietats:
Els subconjunts d’un conjunt donat U formen una àlgebra de Boole amb les operacions de complementació, reunió i intersecció Els elements distingits són el conjunt buit i U En una àlgebra de Boole es pot definir un ordre parcial de la següent manera x ≤ y si, i solament si, x ∧ y = x o, equivalentment, x ∨ y = y Hom ha aplicat l’àlgebra de Boole en teoria de probabilitats, i en el disseny dels circuits elèctrics en què es basen les unitats lògiques dels ordinadors En aquest cas els connectors lògics ∧, ∨ i ¬ són reemplaçats per operacions físiques 1 passa el corrent 0 no passa…
partició d’un conjunt
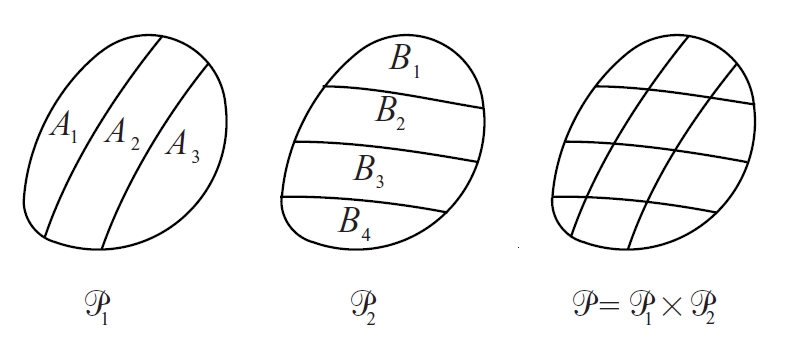
partició d’un conjunt
Matemàtiques
Família de subconjunts d’un conjunt donat, tal que dos subconjunts qualssevol de la família tenen intersecció buida i la reunió de tots els subconjunts de la família és el conjunt donat.
Per exemple, un criteri de veritat indueix una partició en el conjunt de les proposicions el subconjunt de les que són certes i el subconjunt de les que són no certes
univers
Matemàtiques
Conjunt de referència els subconjunts del qual són utilitzats en un raonament concret.
En els diagrames de Venn-Euler hom sol representar l’univers amb un rectangle, dins el qual són dibuixats els diagrames dels conjunts que hom vol representar Així, en l’estudi dels conjunts de nombres reals l’univers és ℝ