Resultats de la cerca
Es mostren 15 resultats
involució
Matemàtiques
Transformació que, essent distinta a la identitat, aplicada dues vegades successivament dóna la identitat.
Una aplicació és involutiva si f = f - 1
regla de L’Hôpital
Matemàtiques
Regla que permet de calcular límits de funcions en el cas d’indeterminacions del tipus 0/0 o ∞/∞.
Segons aquesta regla, el límit del quocient de dues funcions és igual al quocient de llurs derivades, o sia Si el quocient entre les primeres derivades continua essent indeterminat, hom aplica la regla prenent les segones derivades, i així successivament, fins a resoldre la indeterminació
fórmula del trapezi
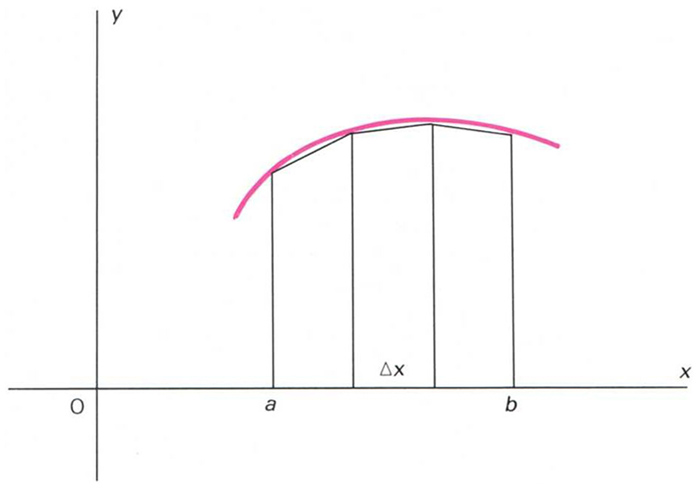
Aplicació de la fòrmula del trapezi
© fototeca.cat
Matemàtiques
Regla utilitzada per a aproximar l’àrea compresa entre una corba, una línia horitzontal i dues de verticals que tallen la corba.
Hom divideix el segment horitzontal en diverses parts iguals i dibuixa les perpendiculars des de cada punt de divisió a la corba després les interseccions d’aquestes rectes amb la corba són unides mitjançant línies rectes, successivament La suma de les àrees dels trapezis així engendrats representa una aproximació de l’àrea limitada per la corba
Henri Cartan
Matemàtiques
Matemàtic francès, fill d’Élie Cartan
.
Graduat i doctorat 1928 a l’École Normale Superieure, des del 1939 fou successivament professor, entre d’altres, a les universitats d’Estrasburg, de la Sorbona 1940-65, i Paris Sud 1969-75 Tingué com a deixebles Jean-Pierre Serre i René Thom Membre fundador del grup Nicolas Bourbaki 1935, treballà en els camps de la geometria diferencial, de la teoria de formes analítiques i de la topologia algèbrica Publicà nombrosos treballs, entre els quals Homological Algebra 1956, amb S Eilenberg Fou membre de l’Acadèmia de Ciències 1974 i president de la Unió Matemàtica Internacional 1967-…
panel
Matemàtiques
Mostra permanent de persones que hom interroga successivament, a intervals regulars, perquè informin sobre l’evolució d’actituds i opinions.
Kunihiko Kodaira
Matemàtiques
Matemàtic japonès.
Doctorat per la Universitat de Tòquio 1949, posteriorment fou professor a Princeton 1949-61 i, fins el 1967, successivament a Harvard, Johns Hopkins i Stanford Aquest any retornà a la Universitat de Tòquio, on es jubilà el 1985 El 1954 rebé la medalla Fields pels seus treballs en geometria algèbrica Dedicat a la topologia, estudià la teoria dels feixos, especialment els fulls de Riemann La seva principal aportació és la demostració del teorema de Roch-Riemann per a les funcions amb un nombre qualsevol de variables teorema de K Publicà Harmonic Integrals 1950, amb G de Rham, On…
Henri Poincaré

Henri Poincaré
© Fototeca.cat
Física
Matemàtiques
Matemàtic i físic francès.
Professor a Caen i des del 1881 a la Sorbona de París, explicà successivament mecànica teòrica, física matemàtica, càlcul de probabilitats i astronomia Dotat d’una intelligència privilegiada, féu aportacions notables en tots aquests camps, des del descobriment de les funcions automorfes fins a l’exposició de la teoria ergòdica Proposà diverses teories fecundes i ha estat considerat com un precursor d’Einstein per les seves intuïcions sobre el principi de la relativitat i l’espai de quatre dimensions Entre les seves obres, publicades íntegrament en edició pòstuma Oeuvres, 11…
semblança
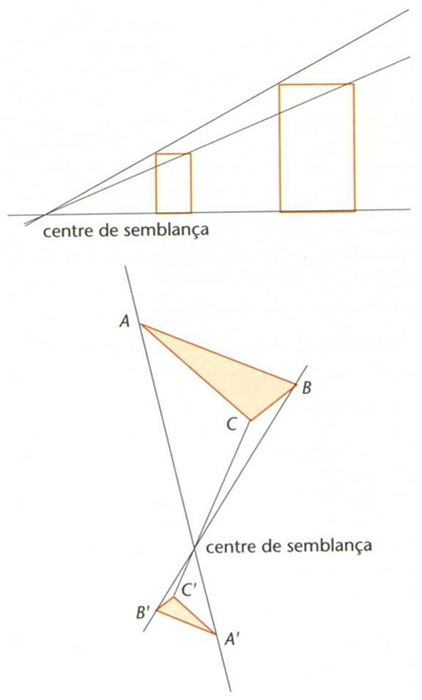
Dues semblances directes
© Fototeca.cat
Matemàtiques
Transformació geomètrica T de ℝn en ℝn tal que la distància entre les imatges de dos punts qualssevol és igual a la distància entre aquests dos punts multiplicada per una quantitat constant positiva dita raó de la semblança.
És a dir, d T x, T y = k, d x, y Dues figures són anomenades semblants si hi ha una semblança que transforma l’una en l’altra Les semblances conserven la forma de les figures però en canvien la grandària, eixamplant-la o reduint-la segons que la raó sigui respectivament major o menor que 1 Les semblances de raó 1 són dites isometries o moviments rígids , els quals són sempre el resultat de compondre una translació amb una transformació lineal ortogonal que conserva els angles Les homotècies són exemples típics de semblances Tota semblança és el resultat d’aplicar successivament…
Heisuke Hironaka
Matemàtiques
Matemàtic japonès.
Estudià a la Universitat de Kyoto, on es graduà en ciències l’any 1954, i obtingué un màster l’any 1956 L’any 1957, a instàncies d' Oscar Zariski , anà a Harvard, on es doctorà el 1960 Posteriorment fou successivament professor a les universitats de Brandeis i Columbia fins el 1968, que es reincorporà a la Universitat de Harvard El 1975 retornà al Japó i fou nomenat professor a l’Institut per a la recerca matemàtica de la Universitat de Kyoto, que dirigí entre el 1983 i el 1985, i on es jubilà 1991 En el període 1996-2002 fou president de la Universitat de Yamaguchi, i…
transformació
Matemàtiques
Aplicació bijectiva d’un conjunt en un altre o en ell mateix.
El conjunt de les transformacions d’un conjunt en ell mateix té estructura de grup respecte a la composició de transformacions la composició en el sentit d’aplicar successivament de manera ordenada dues transformacions és anomenada també producte Segons la definició de Felix Klein, la geometria és l’estudi de les nocions invariants per a un grup de transformacions geometria Com a exemples de transformacions en el pla poden ésser esmentades les rotacions, les simetries axials, les translacions, etc i en l’espai, les simetries respecte a un eix o a un pla, les rotacions axials, etc Segons les…