Resultats de la cerca
Es mostren 9 resultats
Paolo Ruffini
Matemàtiques
Matemàtic i metge italià.
Fou professor a Mòdena Estudià principalment les equacions algèbriques i demostrà la no-solució algèbrica de les equacions de cinquè grau o superiors Publicà Teoria Generale dell’equazione 1799, Memoria sul tifo contagioso i d’altres obres posteriors N'ha estat publicada també l’obra Opere matematiche 1915-54, en 3 volums
derivada parcial d’una funció en un punt
Matemàtiques
Donada una funció real, f:D⊂ℝn→ℝ, i un punt del seu domini de definició, a=(a1,...,an) ∈D, derivada en el punt ai de les funcions d’una variable fi(xi) = f(a1,...,xi,...,an)
.
La i-èsima derivada parcial de f en el punt a és, doncs, el nombre ∂ f/∂x i a = df i /dx i a i Si aquesta és, al seu torn, derivable, hom pot definir derivades parcials d’ordres superiors , com, per exemple, ∂ 2 f /∂ x i ∂x j = ∂∂ f / ∂x i / ∂ x j
Satyendranath Bose
Física
Matemàtiques
Físic i matemàtic indi.
Acabà els seus estudis el 1915, i començà a treballar en el collegi universitari de Calcuta, el primer de l’Índia que féu estudis científics superiors El 1921 deixà Calcuta i s’establí a la Universitat de Dacca i poc després 1924 envià un treball sobre la teoria quàntica a AEinstein, el qual el féu traduir i publicar i n'assenyalà la importància Mantingué contactes amb De Broglie a França i amb Einstein, Max Born i Heisenberg a Alemanya L’aportació més notable de Bose és la seva estadística matemàtica 1925, derivada de les teories de Planck i aplicable a partícules elementals que…
freqüència
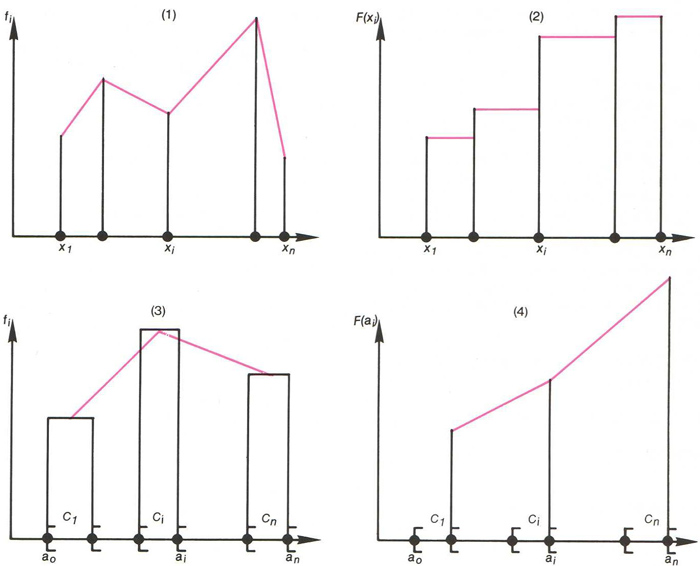
Representacions gràfiques de la freqüència d’una distribució estadística: si el caràcter quantitatiu és discret, (1) és el seu polígon de freqüencies i (2) és la seva corba cumulativa; si el caràcter quantitatiu és continu, (3) és el seu polígon de freqüències i (4) és la seva corba cumulativa
© Fototeca.cat
Matemàtiques
En una distribució estadística d’un caràcter quantitatiu, quocient entre l’efectiu d’un valor concret del caràcter, o d’una classe de valors, i el nombre d’individus que integren la mostra.
Si el caràcter quantitatiu és discret , i pren els valors x 1 ,,x n sobre una mostra de N individus, la freqüència o freqüència relativa del valor x i és el quocient f i = n i / N , on n i és l’ efectiu del valor x i és a dir, el nombre d’individus de la mostra que presenten el valor x i del caràcter La representació gràfica de la funció de distribució x i → f i és una línia poligonal obtinguda en unir els punts de coordenades x i , f i , i =1,, n , anomenada polígon de freqüències Si el caràcter quantitatiu és continu , donada una classe o interval C i = a i - 1 , a i del conjunt de…
espai topològic
Matemàtiques
Conjunt X en el qual s’ha donat una topologia
.
Els conjunts de la família donada són anomenats oberts , i llurs complementaris, tancats Rep el nom d' entorn obert d’un punt tot conjunt obert que el conté Base de l’espai topològic és una família de conjunts oberts que per reunió poden donar qualsevol altre obert Alguns espais topològics tenen llur topologia definida per mitjà d’una distància, la qual determina la base d’oberts de la topologia formada per les boles o esferes En són exemples la recta real ℝ i els espais euclidians de dimensions superiors ℝ n Un subespai d’un espai topològic és una part de l’espai amb la…
topologia

Topologia Les figures unides amb fletxes són topològicament iguals, perquè és possilbe passar de l’una a l’altra per mitjà d’una transformació contínua
© Fototeca.cat
Matemàtiques
Part de la matemàtica que estudia aquelles propietats dels conjunts de punts de la recta, del pla, de l’espai o d’espais de dimensions superiors que no són alterades per les transformacions contínues.
Es tracta de propietats geomètriques que no depenen de cap magnitud, sinó únicament de la posició relativa dels punts Per exemple, el fet que dos punts puguin unir-se o no per un camí, o que el nombre de cares menys el d’arestes més el de vèrtexs d’un políedre esfèric sigui sempre dos teorema d’Euler Aquí hom entén per transformació contínua aquella que admet una inversa i que tant ella com la inversa són contínues L’íntima connexió que hi ha entre el concepte de continuïtat d’una funció en un punt i el d’entorn d’un punt permet de transportar l’estudi de propietats topològiques a aquells…
reticle
Matemàtiques
Conjunt ordenat en el qual dos elements qualssevol tenen un suprem (la més petita de les fites superiors o elements majorants) i un ínfim (la més gran de les fites inferiors o elements minorants).
És anomenat també conjunt reticular Si C, ≤ és un “ordenat” que és reticle, donats a i b de C, existeix un element, anomenat suprem c = a ∪ b tal, que a ≤ c , b ≤ c , i si a < d i b < d és c < d i un element, dit ínfim , c = a ∩ b tal, que c < a, c < b i si d ≤a, d ≤ b , és d ≤ c El conjunt de parts d’un conjunt respecte a l’ordre definit per la inclusió és un reticle Exemple si A i B són dos conjunts qualssevol, el conjunt més petit que els conté és la seva reunió o suprem i el més gran contingut és la seva intersecció o ínfim La teoria de reticles…
Aristòtil

Còpia romana d’Aristòtil del període imperial (segle I o II dC) d’un bronze perdut realitzat per Lísip (Museu del Louvre)
Yuxuan Wang (CC BY-NC-ND 2.0)
Filosofia
Matemàtiques
Filòsof i científic grec, un dels esperits més potents i influents de la història.
Vida i obra Del clan dels asclepíades, era fill de Nicòmac, metge i amic d’Amintes II de Macedònia A divuit anys ingressà a l’Acadèmia Els primers temps fou el deixeble predilecte de Plató, però les divergències posteriors els distanciaren A la mort del mestre 347, Aristòtil abandonà Atenes i passà tres anys a Assos, on s’uní amb Herpillis, de la qual tingué un fill, Nicòmac, al qual dedicà un dels tractats d’ètica D’Assos passà a Mitilene d’aquesta època daten molts dels seus treballs de biologia En 343-342 aC Filip de Macedònia li encarregà l’educació d’Alexandre Aristòtil, que atribuïa una…
espai vectorial
Matemàtiques
Grup abelià E
en el qual hi ha definida una llei de composició externa amb elements d’un cos K
, K
× E
→ E tal, que al parell (λ, e
) correspon l’element λ e
.
I acomplint-se les propietats λ + μ e = λ e + μ e , λ e + f = λ e + λ f , λμ e = λμ e i 1 e = e Els elements de E són anomenats vectors , i els elements de K , escalars Una part de E que sigui subgrup respecte a la suma i que sigui estable respecte al producte per qualsevol escalar, és anomenada subespai de E , i amb les mateixes operacions de E és un altre espai vectorial Si F és un subespai de E , hom pot definir congruències a E mitjançant la relació d’equivalència x ≡ y mòd F , si i només si la diferència x — y pertany a F Això permet de formar el conjunt quocient E/F quocient, el…