Resultats de la cerca
Es mostren 11 resultats
punt de tangència
Matemàtiques
El punt comú a una corba i a una recta que li és tangent o bé a una superfície i a un pla que li és tangent.
punt de tangència
Matemàtiques
Punt de contacte de dues línies, de dues superfícies, tangents.
evolvent
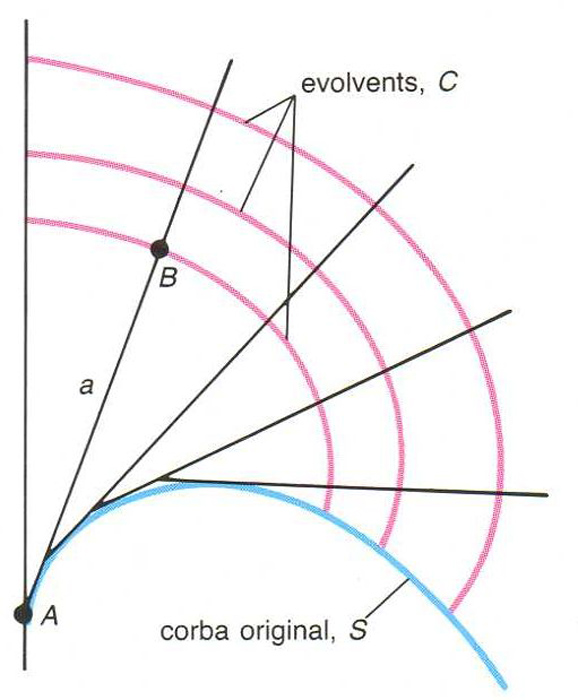
Les corbes C són les evovlents de S
© fototeca.cat
Matemàtiques
Donada una corba S
, cadascuna de les corbes ortogonals a les tangents de S
.
Si C és una envolvent de S , S és l'evoluta C Donada la corba S , hom pot generar una evolvent tot fixant una tangent a S en un punt de tangència A , limitant-ne la seva longitud a i anant-la enrotllant a la corba, de manera que el punt extrem B determina una evolvent Les diferents longituds a determinen les diferents evolvents
evoluta
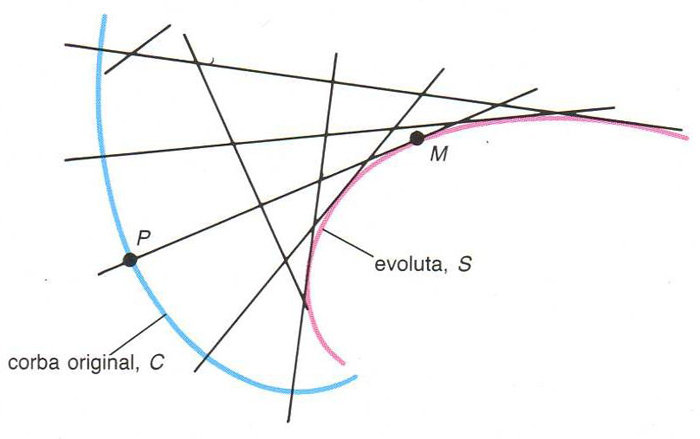
La corba S és l’evoluta de C
© fototeca.cat
Matemàtiques
Donada una corba plana C
, lloc geomètric dels centres de curvatura de C
.
És l'envolupant S de les normals a la corba C així, una normal en el punt P a C és tangent a l’evoluta i el punt de tangència M és el centre de curvatura de C en el punt P Si S és l’evoluta de C , C és una evolvent de S L’evoluta d’un cercle es redueix a un punt
clotoide
Construcció i obres públiques
Matemàtiques
Corba d’acord o de transició en planta resolta amb la clotoide.
Per la propietat que la defineix, un vehicle ideal que la recorre a velocitat constant és sotmès a un acceleració centrífuga uniformement variable, directament proporcional a la distància recorreguda entre el punt de tangència amb la recta valor 0 i un punt determinat valor V 2 /R Per aquesta raó, és la corba d’acord més utilitzada en el traçat en planta de ferrocarrils i carreteres per a passar d’una alineació recta a una corba circular o d’una corba circular a una altra d’un radi diferent És definida pel paràmetre que li correspon Hi ha plantilles especials per a dibuixar-la i…
cissoide de Diocles
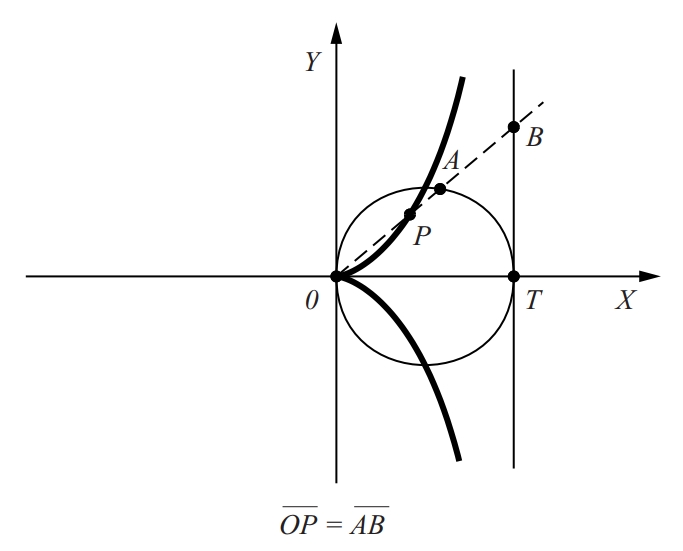
cissoide de Diocles
Matemàtiques
Cissoide associada amb una circumferència, a una recta tangent i a un punt fix O diametralment oposat al punt de tangència.
Fou construïda per Diocles per resoldre la duplicació del cub La seva equació cartesiana és y 2 2 k – x = x 3 Es tracta, doncs, d’una cúbica
bitangent
Matemàtiques
Dit d’una línia o superfície que té dos punts de tangència amb la línia o superfície a la qual és tangent.
tractriu
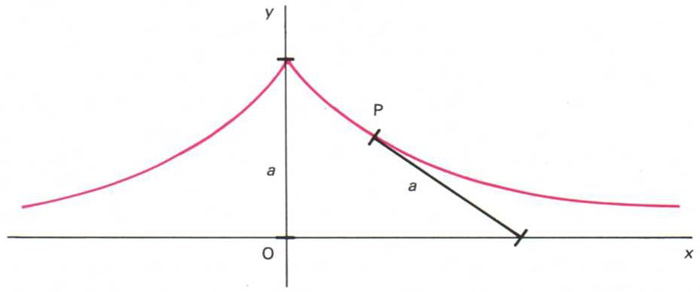
fototeca.cat
©
Matemàtiques
Corba tal, que totes les seves tangents tenen la mateixa longitud a
, compresa entre el punt de tangència P i l’eix OX.
La seva equació és La tractriu és la involuta d’una catenària