Resultats de la cerca
Es mostren 74 resultats
tangent
circumferències tangents
Matemàtiques
Que toca en un sol punt una línia o una superfície.
Dues circumferències tangents
arc tangent
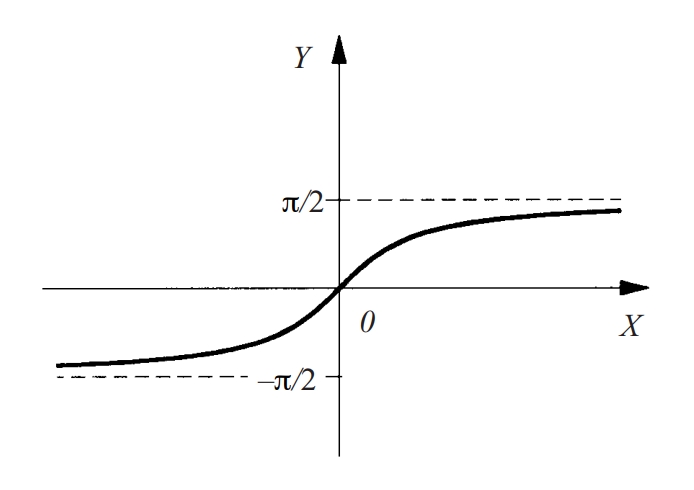
arc tangent
recta tangent

recta tangent a una corba en un punt
Matemàtiques
Recta que passa per un punt P d’una corba o d’una superfície i és la posició límit d’una recta variable que passa per aquest punt i per un altre de la mateixa corba o superfície que es mou fins a coincidir amb el primer.
Si l’equació de la corba plana és y = f x , la tangent en el punt P x 0 , f x 0 és la recta y-f x 0 = f' x 0 x-x 0
funció tangent
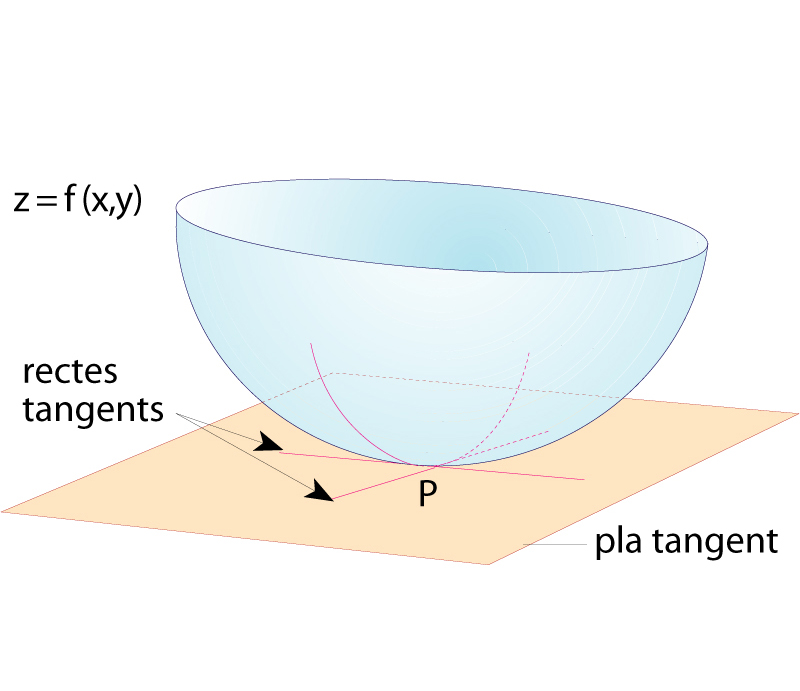
Pla tangent i dues rectes tangents a la superfície z=f(x,y) en el punt P
© Fototeca.cat
Matemàtiques
Funció tg: →-{π/2+kπ, k ∈ℤ} →ℝ, definida per l’assignació x
→tg x
, on tg x
és la tangent de l’angle que fa x
radiants.
És una funció periòdica de període 2 i el seu recorregut és -∞, ∞ És una de les sis funcions trigonomètriques o circulars i està relacionada amb les funcions sinus i cosinus per l’expressió tg x =sin x /cos x És indefinidament derivable i el seu desenvolupament en sèrie entera és quan x 2
vector tangent
Matemàtiques
Donada una corba qualsevol x=x(t), y= y(t), z=z(t), i un punt [x(t0), y(t0), z(t0)], vector paral·lel a [x’(t0), y’(t0), z’(t0)] i de mòdul unitat.
La recta que, passant pel punt x t 0 , y t 0 , z t 0 té per vector director el vector tangent, és anomenada recta tangent a la corba , amb la qual cosa hom generalitza la noció de recta tangent a una corba plana per al cas de les corbes guerxes
pla tangent
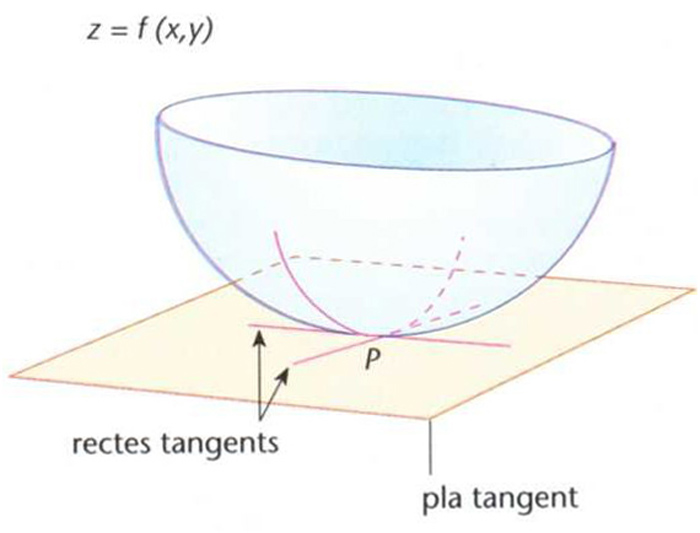
Pla tangent i dues rectes tangents a la superfície z= f(x,y) en el punt P
© Fototeca.cat
Matemàtiques
Donada una superfície z=f(x,y) i un punt P [x0, y0f(x0, y0)], pla que conté les rectes tangents en aquest punt a totes les corbes contingudes en la superfície considerada i que passen pel punt [x0, y0, f(x0, y0)].
L’equació d’aquest pla és
funció tangent hiperbòlica
Matemàtiques
Funció th: ℝ→ℝdefinida per l’assignació x →thx, on th x és la tangent hiperbòlica del nombre real x.
funció tangent complexa
Matemàtiques
Funció tg: ℂ-{(k+1/2)π, k ∈ℤ} →ℂ, definida per l’assignació z →tgz = (sinz)/(cosz), on sin z és la funció sinus complex i cos z la funció cosinus complex.
Hom pot comprovar que tg z = e 2 i z - 1 / i e 2 i z + 1
tangent d’un angle
Matemàtiques
Donats dos eixos perpendiculars x i y, i una circumferència de radi unitat centrada en el punt d’intersecció dels eixos (cercle goniomètric), i un segment que forma un angle α amb l’eix d’abcisses x, longitud del segment, perpendicular a l’eix d’abcisses, deteminat entre el punt de la circumferència de coordenades (1,0) i el punt en què aquest segment s’interseca amb el segment inclinat l’angle α en qüestió.
Aquesta longitud és la tangent de l’angle α, i és denotada per tgα És vàlida la següent igualtat tgα=sin α/cos α, on sin és el sinus d’un angle i cos és el cosinus d’un angle La tangent de l’angle α determinat entre dos segments qualssevol és la tangent de l’angle que, dibuixat sobre el cercle goniomètric, té la mateixa obertura que α Algunes fòrmules trigonomètriques relatives a la tangent d’un angle són tgα+β=tgα+tgβ/1-tgα- tgβ tg-α=-tgα tgα+tgβ- =sinα+β/cosα cosβ
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- Pàgina següent
- Última pàgina