Resultats de la cerca
Es mostren 4 resultats
covariant
Matemàtiques
Dit dels tensors d’ordre superior a 1 les components dels quals es transformen, en un canvi de coordenades, segons la matriu del canvi de base.
Per exemple, si és un canvi de base de l’espai vectorial en qüestió, les components d’un vector v covariant es transformen com Les components o coordenandes d’un vector covariant són indexades mitjançant subíndexs v μ
contravariant
Matemàtiques
Dit dels tensors d’ordre superior a 1 les components dels quals es transformen, en un canvi de coordenades, segons la matriu inversa del canvi de base.
Per exemple, si e ' v = A µ v e µ és un canvi de base de l’espai vectorial en qüestió, les components d’un vector v contravariant es transformen com v ' µ = A - 1 µ v v Les components o coordenades d’un vector contravariant són indexades mitjançant superíndexs v µsup
homotècia
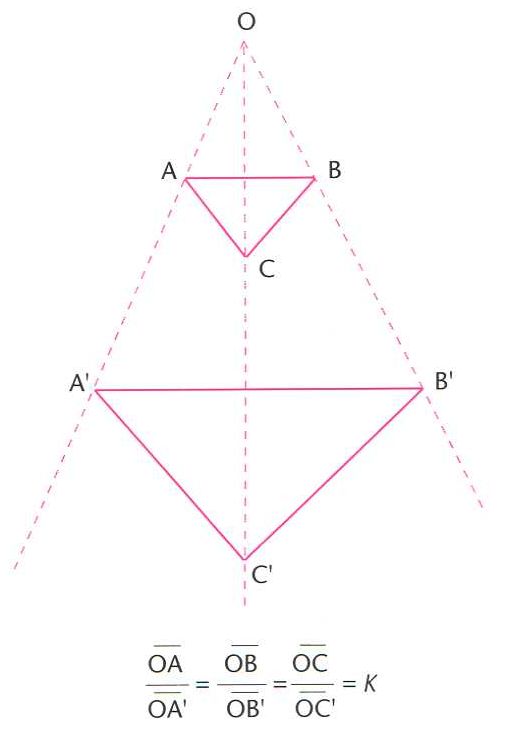
Homotècia, transformació homotètica d’un triangle ABC (O, centre de l’homotècia; k, raó d’homotècia)
© Fototeca.cat
Matemàtiques
Transformació geomètrica del pla o de l’espai que compleix aquestes dues condicions.
Qualsevol punt A i la seva imatge A' són alineats amb un punt fix O anomenat centre d’homotècia , i els segments compleixen la relació k essent, per a cada homotècia, una constant real anomenada raó de l’homotècia Les homotècies transformen rectes en rectes, circumferències en circumferències i conserven els angles
projectivitat
Matemàtiques
Transformació projectiva, és a dir, aplicació injectiva entre dos plans projectius no necessàriament diferents (f: p* →p*’, que transforma conjunts de punts col·lineals en conjunts de punts col·lineals.
L’estudi de les propietats del pla projectiu invariants sota una projectivitat són l’objecte d’estudi de la geometria projectiva Si f és una projectivitat, es demostra que el transformat x' , y' d’un punt x , y es troba per les equacions i que tota transformació donada per les anteriors equacions és una projectivitat plana, és a dir, que els punts x, y tals que a 3 x + b 3 y + c 3 = 0 es transformen en els punts impropis del pla projectiu