Resultats de la cerca
Es mostren 6 resultats
integral triple
Matemàtiques
Integral múltiple en el cas particular n=3.
És notada per ∫∫∫ D f x,y,z dxdydz
integral múltiple
Matemàtiques
Integral definida sobre un domini D de ℝn.
Donat un domini D de ℝ n , i una partició en dominis elementals D i d’àrees a i i diàmetres d i , i donada una funció real definida sobre D , fD ⊂ ℝ n → ℝ, límit I quan els d i tendeixen a 0, de les sumes de Riemann on A i ∈ D i Hom diu que I és la integral de f en D i és notada per ʃ ʃ n ʃ D ʃ x 1 , x n d x 1 dx n Els casos particulars n =2 i n =3 constitueixen la integral doble i la integral triple, respectivament Les integrals múltiples poden ésser calculades per integració unidimensional reiterada
deltoide
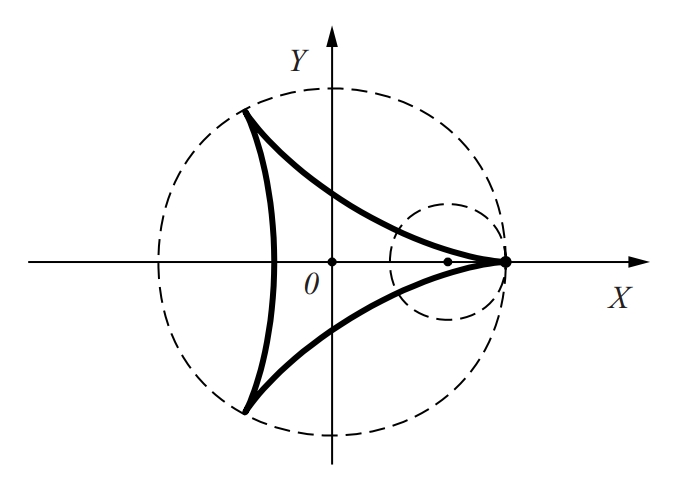
deltoide
Matemàtiques
Hipocicloide d’un cercle de radi k que roda, sense lliscar, dintre d’un altre que té el radi triple.
Les seves equacions paramètriques són x = k 2cos t + cos 2t , i y = k 2sin t + sin 2 t
volum
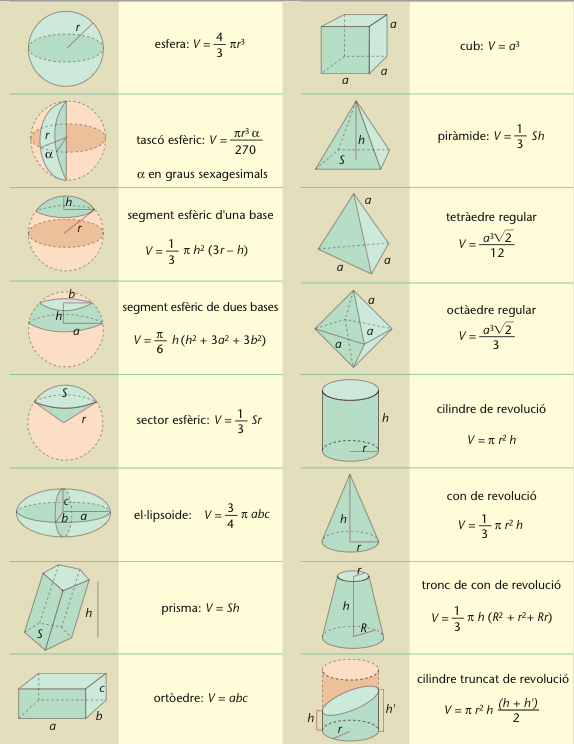
Fórmules per al càlcul de volums
© Fototeca.cat
Matemàtiques
Grandor o mesura de la porció de l’espai ocupada per un cos.
El volum és una mesura que a tota regió de l’espai de tres dimensions assigna un nombre real positiu, de manera que es compleix la propietat additiva, és a dir, que el volum d’un cos és igual a la suma dels volums de qualsevol partició que hom hagi fet en el cos divisió del cos en parts disjuntes Prenent com a base que el volum assignat a un cub de costat a és a 3 , el volum de qualsevol altre cos pot ésser calculat com l’ínfim de la suma dels volums dels cubs disjunts que plegats cobreixen el cos Així, el volum d’una figura plana és zero El volum dels cossos geomètrics simples pot ésser…
integral
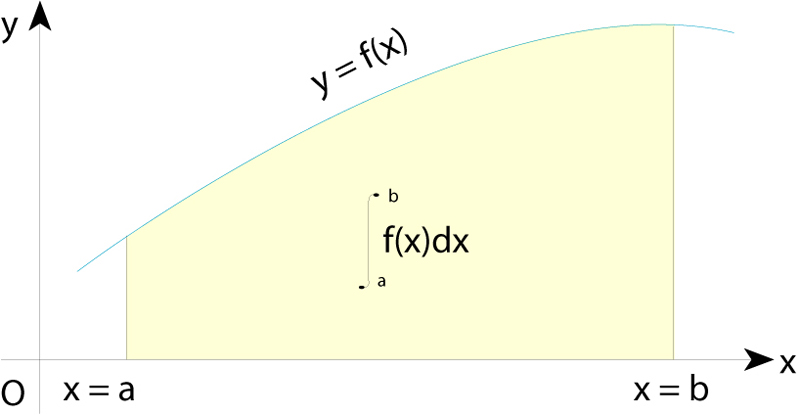
El valor d’una integral definida és igual a l’àrea limitada per la funció, l’eix d’abcisses i les dues ordenades corresponents als extrems de l’interval de definició
© Fototeca.cat
Matemàtiques
En el sentit més general, forma lineal μ sobre certs espais vectorials de funcions, que assigna a cada funció f de l’espai un escalar μ(f) anomenat integral de f.
Hom distingeix entre tres tipus fonamentals d’integral, la integral de Riemann , la integral de Riemann-Stieltjes i la integral de Lebesgue La integral de Riemann té una interpretació geomètrica simple per tal com fou definida a fi de calcular àrees i volums de figures geomètriques Si a,b és un interval tancat de la recta real, i P={ x 0 ,, x n } és una partició de a,b , és a dir, un conjunt finit de punts tal que a = x 0 ≤ x 1 ≤ ≤ x n = b , sigui Δ x i = x i - 1 per a i =1,, n Si f és una funció fitada definida en a, b , hom determina en cada subinterval x i - 1 , x i els termes M i…