Resultats de la cerca
Es mostren 7 resultats
base dels índexs
Matemàtiques
Valor estadístic emprat com a referència de les expressions que permeten el càlcul dels índexs numèrics, corresponent a la intensitat o a la mitjana de la intensitat d’un determinat fenomen en un lloc i durant un cert període de temps.
En una sèrie cronològica hom anomena any-base l’escollit com a referència i que té assignat un índex, usualment de valor 100
bola
Matemàtiques
En un espai mètric amb una distància d, conjunt de punts x la distància dels quals a un cert punt fix a és menor (o igual) que un nombre fix r (r > 0); es parla, aleshores, de la bola oberta (tancada) de radi r i de centre a.
Usualment es denota per B a r la bola oberta i per B̄ a r la bola tancada A ℝ les boles obertes són els intervals oberts i les boles tancades són els intervals tancats
autòmat finit determinista
autòmat finit determinista
Matemàtiques
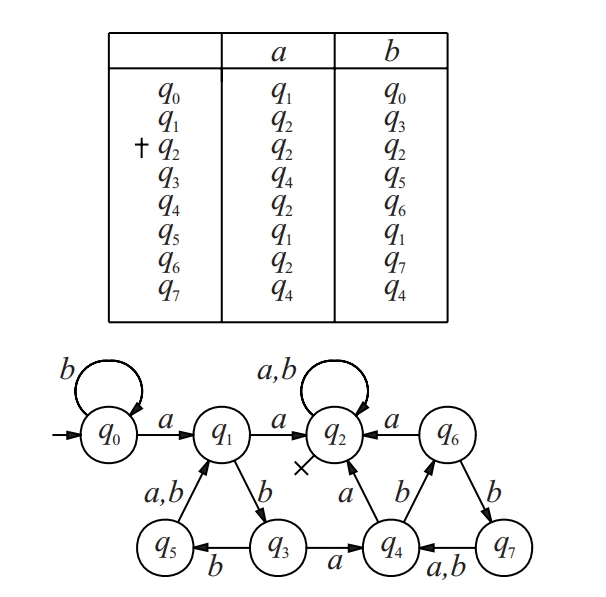
Estructura de la forma M = (Q, ∑, δ, q0, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet, anomenat d’entrada; δ : Q ⨉ ∑* → Q és la funció de transició que satisfà ∀q ∈ Q, ∀x,y ∈ ∑*:δ(q, λ) = q, δ(q, xy) = δ(δ(q, x), y) essent xy la concatenació de x i de y, i λ la paraula buida i ∑* el conjunt de paraules; q0 ∈Q s’anomena estat inicial; F ⊂ Q s’anomena conjunt d’estats finals o acceptadors.
Usualment un autòmat finit determinista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si δ q i , a = q j S’indica l’estat inicial amb una fletxa i els finals amb una creu
autòmat finit indeterminista
autòmat finit indeterminista
Matemàtiques
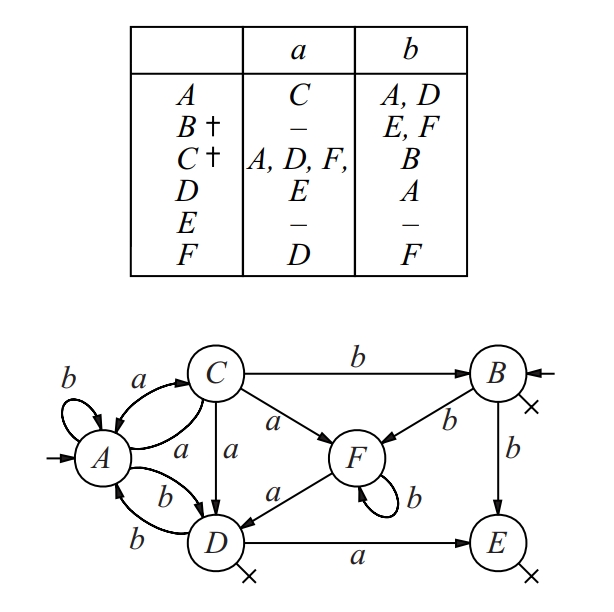
Estructura de la forma M = (Q, ∑, δ, I, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet anomenat d’entrada; δ : 2Q ⨉ ∑* → 2Q és la funció de transició que satisfà ∀P1, P2 ⊂ Q, ∀x, y∈∑*: δ(∅, x) = ∅, δ(P1, λ) = P1, δ(P1 ∪ P2, x) = δ(P1, x) ∪ δ(P2, x), δ(P1, xy) = δ(δ(P1, x)y), essent xy la concatenació de x i de y i ∑* el conjunt de paraules; I ⊂ Q és el conjunt d’estats inicial; F ⊂ Q és el conjunt d’estats finals o acceptadors.
Usualment un autòmat finit indeterminista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si q j ∈ δ q i , a S’indiquen els esstats inicials amb fletxes i els finals amb una creu Els llenguatges acceptats pels autòmats finits indeterministes són els mateixos que els reconeguts pels finits deterministes regulars L’avantatge dels indeterministes enfront dels deterministes és la facilitat de maneig i de construcció
arc
Matemàtiques
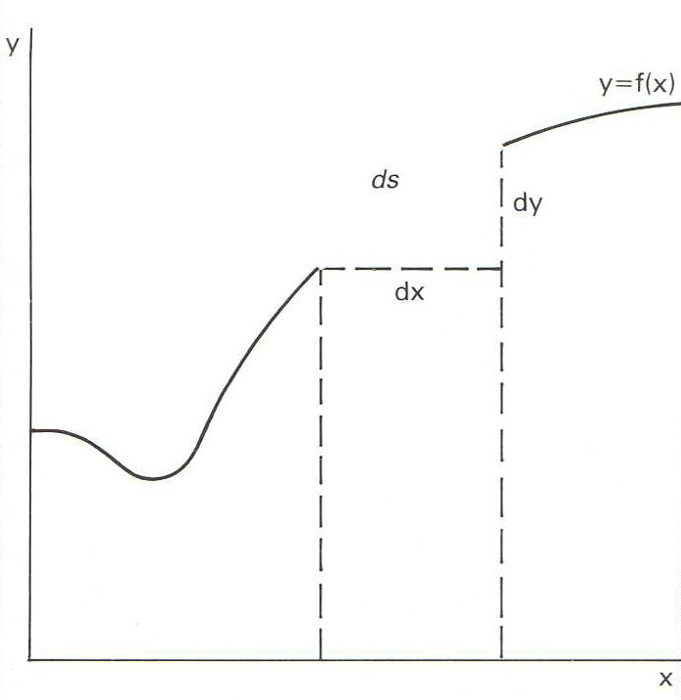
Segment o part d’una corba.
Usualment també designa una corba oberta completa Les característiques d’un arc llargada, corda, fletxa depenen de la corba a la qual pertany En el cas d’una circumferència, hom mesura els arcs en unitats d'angle i un arc val igual que l'angle en el centre que el limita en trigonometria, però, hom considera a vegades que un arc de circumferència α, mesurat en radians, admet una infinitat de determinacions que difereixen per un nombre enter de circumferències i són donades per la fórmula α + 2 k π, on k pot ésser zero o un enter qualsevol El principal problema que es planteja a…
taula
Matemàtiques
Llista sistemàtica de resultats (ja obtinguts) que facilita el treball posterior de maneig de les dades.
Usualment hi ha les llistes d’un cert nombre de valors d’una variable i els valors corresponents d’una altra que és funció de la primera, els quals són disposats generalment en columnes paralleles aquesta configuració final és anomenada taula de la funció En són exemples la taula de quadrats, de cubs, de logaritmes, de sinus, de cosinus, de tangents, de paràmetres astronòmics, etc La taula de sumar o de multiplicar pot ésser feta usant un quadrat dividit en 81 cases quadrades disposades formant nou files i nou columnes les 9 cases de la primera fila i les 9 de la primera…
nomograma
Matemàtiques
Gràfic o àbac que consisteix en tres (o més) línies rectes (de vegades corbes), usualment paral·leles i graduades cadascuna per una variable de manera que, en tallar les tres línies amb una recta ortogonal, hom obté els valors relatius de les tres variables.