Resultats de la cerca
Es mostren 13 resultats
tríedre
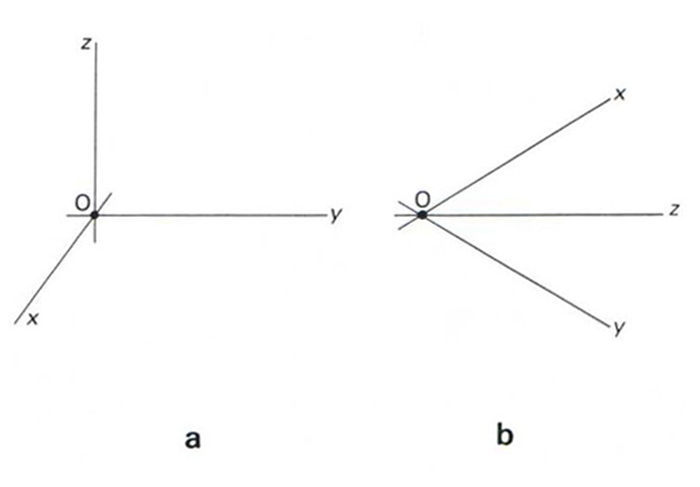
tríedre: a, triectangular; b, guerxo
© fototeca.cat
Matemàtiques
Figura formada per tres línies no coplanàries que es tallen en un punt.
Tot tríedre pot ésser descrit en termes de tres plans que es tallen en un punt i és la base per a utilitzar sistemes de referències amb coordenades És anomenat tríedre trirectangular si les línies que el determinen són perpendiculars
Robert Recorde
Matemàtiques
Matemàtic anglès.
Estudià a Oxford i Cambridge Fou autor de diversos llibres de text que foren usats a les escoles angleses durant més de cent anys Fou el primer a utilitzar el signe = Publicà també obres d’astronomia, com The Castle of Knowledge 1551
perspectiva lineal
Art
Disseny i arts gràfiques
Matemàtiques
Perspectiva que representa els objectes en qualsevol dels sistemes perspectius, utilitzant com a mitjà d’expressió solament la línia.
La perspectiva lineal, en cenyir-se al contorn dels objectes, dóna una imatge precisa, i per això és la més utilitzada per a traçats geomètrics, plànols i dibuixos tècnics Té, però, l’inconvenient de no utilitzar el clar-obscur ni el color, per la qual cosa sol resultar freda i rígida
teorema de Pitàgores
Matemàtiques
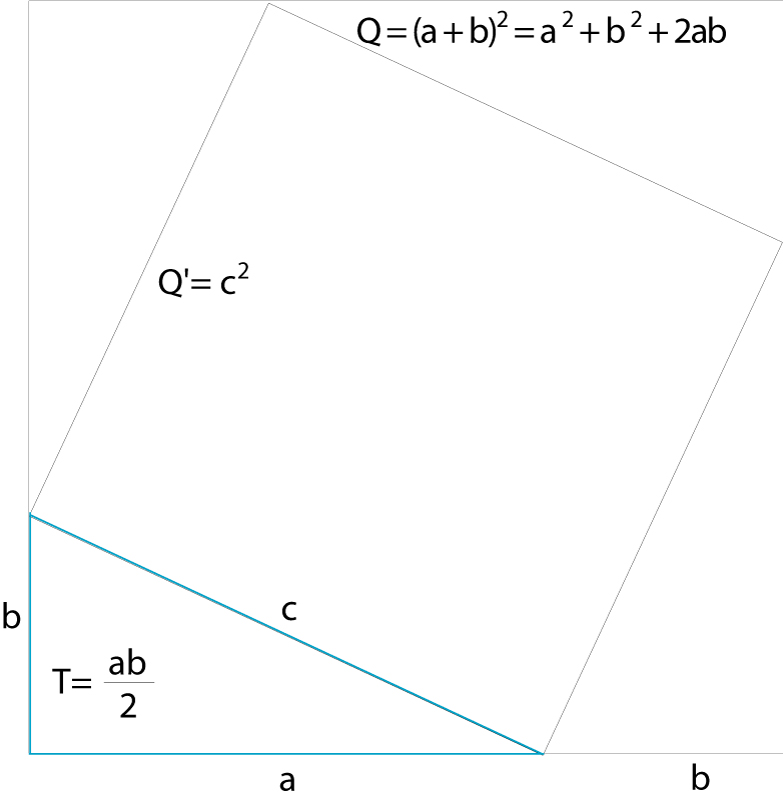
Teorema fonamental de la geometria segons el qual en un triangle rectangle l’àrea del quadrat que té per costat la hipotenusa és igual a la suma de les àrees dels quadrats que tenen per costat els catets.
Si a i b representen les longituds dels catets i c la longitud de la hipotenusa, el teorema Pitàgores és expressat per la igualtat c 2 = a 2 + b 2 Bé que la primera demostració del teorema sembla que fou feta pels membres de l’ escola pitagòrica Pitàgores vers l’any 550 aC, el teorema de Pitàgores, almenys en alguns casos particulars, ja era conegut pel poble egipci vers l’any 2000 aC, pels xinesos vers l’any 1100 aC i pels vedes vers l’any 800 aC D’altra banda, fou a partir del teorema que els pitagòrics descobriren que no n'hi ha prou amb els nombres enters i fraccionaris…
mostra
Matemàtiques
Porció finita d’una població que és utilitzada per a extrapolar conclusions sobre diverses característiques de la població total.
En general, l’elecció d’una mostra estadística és duta a terme amb bases aleatòries, puix que tots els elements de la població han de gaudir de la mateixa probabilitat de formar part de la mostra, les dimensions de la qual són molt variables i depenen de les característiques pròpies del poblema que estadísticament hom vol estimar En mesurar una característica en una mostra hom obté els valors mostrals o distribució empírica de la mostra, de la qual hom extreu els paràmetres estadístics essencials, és a dir, la mitjana, la variància, la mediana, etc, que són els que permeten d’extreure…
nombre real
Matemàtiques
Cadascun dels nombres que hom pot obtenir en mesurar magnituds contínues.
Hom obté el conjunt dels nombres reals completant el conjunt dels nombres racionals amb tots els nombres irracionals que poden ésser representats sobre la recta, tals com etc La manera més simple d’introduir teòricament i d’utilitzar en la pràctica els nombres reals és per mitjà de llur expressió decimal Tot nombre real és expressat en forma decimal amb infinites xifres que, en el cas dels nombres irracionals, no es repeteixen periòdicament Això suposa que per a definir un nombre real cal donar una llei que permeti d’obtenir tantes xifres decimals com hom vulgui A la pràctica,…
trigonometria

1, circumferència de referència per a la definició de les raons trigonomètriques; 2, representació gràfica de les línies trigonomètriques; 3, símbols emprats en la resuloció de triangles
© fototeca.cat
Matemàtiques
Part de la matemàtica inicialment dedicada a l’estudi de les relacions entre les amplituds dels angles i les longituds dels segments que llurs costats determinen en les rectes que tallen.
La trigonometria es basa en les propietats de les anomenades raons trigonomètriques , que són definides a partir d’un punt P x,y d’una circumferència de centre O i per l’angle α que forma el radi r = OP amb l’eix OX , mitjançant els sis quocients següents sin α = y/r sinus cos α = x/r cosinus tg α = y/x tangent cotg α x/y cotangent sec α = r/x secant cosec α = r/y cosecant Quan el punt P és a una distància r = 1 de l’origen O , el valor absolut d’aquestes raons és representat per la longitud de certs segments anomenats línies trigonomètriques , respectivament, fàcils de traçar A partir de…
logaritme
Matemàtiques
Donat un nombre b, real, positiu i distint d’1 (anomenat base), i un nombre qualsevol n real i positiu, nombre a tal, que b, elevat a a, és igual a n, o sia, ba= n.
Hom l’anomena logaritme de base b de n , i el representa per log b n = a Les propietats fonamentals dels logaritmes són Els logaritmes constitueixen un instrument matemàtic que facilita i abreuja molts càlculs complicats Els més utilitzats correntment en el càlcul són els logaritmes decimals, vulgars o de Briggs , que són els logaritmes de base 10 i que hom representa amb els símbols log 1 0 , log o lg Per contra, en els càlculs diferencial i integral són utilitzats els logaritmes naturals o neperians , que són els logaritmes de base e , i hom els representa amb els símbols log e , ln o L…
numeració
Matemàtiques
Art d’expressar tots els nombres amb un conjunt finit de mots i de signes.
El sistema de numeració de l’antic Egipte III millenni aC era decimal , o de base 10, és a dir, hom comptava per unitats, desenes, centenes, etc La unitat, la desena, la centena i el miler eren representats, respectivament, amb els símbols ∣, ⋂, ℮, aquest símbols, fins que la suma de valor dels signes escrits era igual al nombre per exemple, el nombre 1235 era ℮℮⋂⋂⋂∣∣∣∣∣ El sistema de numeració babilònic era de base seixanta i ja utilitzava una notació posicional, cosa que suposa la introducció del zero Era, doncs, un sistema essencialment semblant a l’actual, bé que confusionari, puix que,…
tensor
Física
Matemàtiques
Objecte abstracte que posseeix un determinat sistema de components en cada sistema referencial que hom consideri i tal que, sota transformacions de coordenades, les seves components variïn d’acord amb una transformació predeterminada.
Si E és un espai vectorial de dimensió n sobre un cos algèbric K , hom defineix el tensor covariant d’ordre r com una aplicació T r definida en E x E x r x E = E r , i per a valors en K tal que és lineal en cada component, és a dir, que per a i = 1, 2, 3, , r es compleix a T r x 1 , , x i + y i , , x r = T r x ₁ , , x i ,, x r + T r x 1 , , y i , , x r b T r x ₁ , , λ x i , , x r = λ T r x ₁ , , x i , , x r Els tensors covariants d’ordre 1 formen l’espai E *, anomenat dual de E , és a dir, el conjunt d’aplicacions lineals de E en K E * és, alhora, un espai vectorial de dimensió…