Resultats de la cerca
Es mostren 12 resultats
valuació
Matemàtiques
Funció que fa correspondre a cada proposició el seu valor de veritat, si aquest existeix.
En el cas de la lògica binària clàssica els únics valors de veritat que s’admeten són veritat 1 i fals 0, però en les lògiques polivalents hom accepta un tercer valor 1/2 que admet interpretacions diverses per exemple, possible o indeterminat La taula de veritat bivaluada o polivalent de dues proposicions reflecteix totes les possibles valuacions o assignacions de valors de veritat
tautologia
Lògica
Matemàtiques
Qualsevol fórmula lògica que, en un sistema lògic donat, admet només el valor de veritat.
Així, la fórmula A ∨B ↔&IsbA →B és una tautologia És a dir, si dues proposicions formen una tautologia, és que són lògicament identificables i, per tant, tenen el mateix valor de veritat
paradoxa
Lògica
Matemàtiques
Enunciat o raonament que porta a dues conclusions mútuament contradictòries però de cap de les quals hom no pot prescindir.
Sovint identificable amb l'antinòmia i àdhuc amb l'aporia, la paradoxa, que té un significat més ampli que l’una i l’altra, sol ésser tipificada en l’afirmació del mentider, quan diu “ara dic mentida” si és veritat que diu mentida, és que menteix, però està dient la veritat, o sia que no està mentint i, si no és veritat que diu mentida, menteix, però no és veritat que digui mentida Les paradoxes d’aquesta mena, consistents en una autoreferència i que solen ésser típiques en les anomenades paradoxes semàntiques o lingüístiques, han estat…
partició d’un conjunt
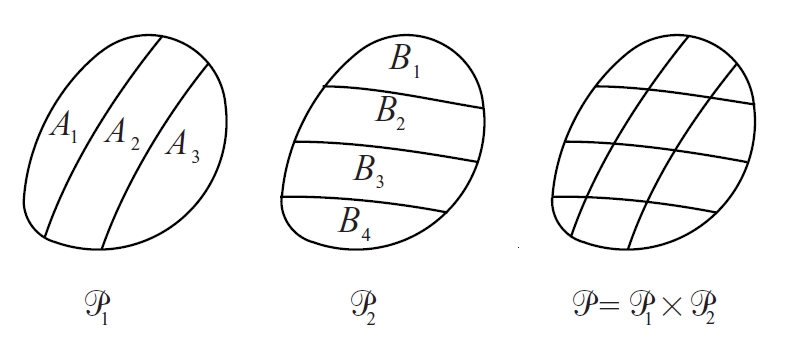
partició d’un conjunt
Matemàtiques
Família de subconjunts d’un conjunt donat, tal que dos subconjunts qualssevol de la família tenen intersecció buida i la reunió de tots els subconjunts de la família és el conjunt donat.
Per exemple, un criteri de veritat indueix una partició en el conjunt de les proposicions el subconjunt de les que són certes i el subconjunt de les que són no certes
Emil Post
Lògica
Matemàtiques
Matemàtic i lògic nord-americà, d’origen polonès.
Introduí un mètode per a controlar les fórmules de la lògica seqüencial mitjançant les taules de veritat És conegut pel fet d’haver proposat el 1920 els sis temes lògics polivalents, especialment trivalents, amb independència de Łukasiewicz Establí també una teoria general de les proposicions elementals 1922, i estudià els problemes dels grups de mots en el llenguatge, amb independència dels resultats obtinguts per Markov
axioma
Filosofia
Matemàtiques
Proposició que hom admet sense demostració com a punt de partença d’una teoria o ciència.
Per a Aristòtil i fins a l’època moderna, els axiomes eren els principis evidents i irreductibles que constituïen els fonaments d’una ciència Actualment, sota la influència de la matemàtica moderna, els axiomes són els enunciats primitius anomenats també, a vegades, postulats acceptats com a vàlids sense provar-ne la veritat, dels quals deriven d’altres proposicions que s’organitzen en un sistema
demostració
Lògica
Matemàtiques
Derivació d’un enunciat, mitjançant l’aplicació d’unes determinades regles lògiques, a partir d’uns altres enunciats, dits premisses de la demostració.
Qualsevol cadena de demostracions ha d’arrencar d’un conjunt finit de premisses no demostrables, els axiomes Aquest conjunt és anomenat el sistema dels axiomes de la teoria deductiva, i els enunciats que són demostrats a partir dels axiomes s’anomenen teoremes Identificada, en la teoria platònica, amb la definició, Aristòtil la considerà com un procés superior, adreçat a extreure, mitjançant el sillogisme, una conclusió a partir d’unes premisses certes L’escolàstica s’adherí a l’esquema aristotèlic i n'elaborà una classificació propter quid , ad intellectum , ad sensum , a priori , a…
taula
Matemàtiques
Llista sistemàtica de resultats (ja obtinguts) que facilita el treball posterior de maneig de les dades.
Usualment hi ha les llistes d’un cert nombre de valors d’una variable i els valors corresponents d’una altra que és funció de la primera, els quals són disposats generalment en columnes paralleles aquesta configuració final és anomenada taula de la funció En són exemples la taula de quadrats, de cubs, de logaritmes, de sinus, de cosinus, de tangents, de paràmetres astronòmics, etc La taula de sumar o de multiplicar pot ésser feta usant un quadrat dividit en 81 cases quadrades disposades formant nou files i nou columnes les 9 cases de la primera fila i les 9 de la primera columna contenen…
demostració per recurrència
Matemàtiques
Mètode de demostració que consisteix a demostrar que una proposició és veritable per a 1 i que si és veritat per a n tamb é ho és per a n + 1.
D’això hom dedueix que la proposició és veritable per a tot n
René du Perron Descartes
Filosofia
Matemàtiques
Filòsof i científic francès.
Conegut també amb el nom llatinitzat de Cartesius , és considerat generalment com el pare de la filosofia moderna Fill d’un conseller del parlament de Bretanya, fou educat al collegi dels jesuïtes de La Flèche, i es llicencià en dret a Poitiers Desitjós de conèixer “el llibre del món”, el 1618 començà un llarg període de viatges, primerament com a soldat i després com a particular Per assegurar-se una vida tranquilla de meditació i estudi, el 1628 es retirà a Holanda, on romangué més de vint anys, fins que, acceptant la invitació de la reina Cristina de Suècia, es traslladà a Estocolm, on…