Resultats de la cerca
Es mostren 16 resultats
Georg von Purbach
Astronomia
Matemàtiques
Matemàtic i astrònom austríac.
Professor a diverses ciutats d’Itàlia i a Viena, on tingué com a deixeble Johann Müller Inicià la traducció al llatí de l' Almagest de Ptolemeu, que després completà el seu deixeble Confeccionà la taula dels sinus i fou un dels primers a emprar-los en trigonometria
Richard von Mises
Matemàtiques
Matemàtic i enginyer austríac, naturalitzat nord-americà.
Germà de Ludwig von Mises, féu contribucions en el camp de l’aerodinàmica, que aplicà a avions de combat dissenyats per a l’exèrcit alemany i pilotats per ell a la Primera Guerra Mundial Professor de matemàtica aplicada a les universitats d’Estrasburg 1909-19 i de Berlín des del 1920, el 1933 abandonà Alemanya per installar-se als EUA, on, des del 1939, fou professor de la Universitat de Harvard Integrat en l’equip dels “Annals of Mathematical Statistics”, féu aportacions al camp de l’estadística matemàtica, com ara la teoria dels collectius
Johannes von Neumann
Matemàtiques
Matemàtic hongarès naturalitzat nord-americà.
Fou un dels pocs matemàtics moderns que reeixí alhora en l’estudi de qüestions de teoria pura teoria de conjunts continuant les investigacions de Zermelo, àlgebra topològica, teoria dels jocs anomenats estratègics , formulació axiomàtica de la mecànica quàntica, etc i en la matemàtica aplicada calculadors electrònics amb “memòria” contenint no sols les dades numèriques d’un problema, sinó també les instruccions que permeten de resoldre'l, com l’EDVAC del 1945, i especialment les màquines autoreproductores, que imiten procediments naturals apresos de la genètica, ideades l’any 1952 És autor,…
Ladislaus von Bortkiewicz
Economia
Matemàtiques
Economista i estadístic alemany d’origen polonès, de l’escola de Lexis.
Els seus principals treballs es refereixen a la teoria del valor, a DRicardo, JRodbertus, KMarx i EBöhm-Bawerk La seva principal aportació és exposada en Wertrechnung und Preisrechnung im marxchen System ‘Càlcul del valor i càlcul del preu en el sistema marxista’, 1906-07, redescoberta per JASchumpeter i PSweeny Seguint bàsicament l’argumentació d’IDmitriev, aquesta ‘teoria de la deducció’ Abzugstheorie , recollida pels economistes soviètics, considera que la relació de salari determina el benefici i no el capital
Paul Isaak Bernays
Lògica
Matemàtiques
Matemàtic i lògic suís.
Coautor amb D Hilbert dels Grundlagen der Mathematik 1934-39 En teoria de conjunts formulà un sistema axiomàtic, sobre la base del de von Newmann, que fou posteriorment estudiat per K Gödel sistema de von Neumann-Bernays-Gödel , i que distingia entre classes i conjunts Axiomatic Set Theory , 1958
Jakob Steiner
Matemàtiques
Matemàtic suís.
Analfabet fins a 14 anys, estudià amb Pestalozzi, i després a Heidelberg i Berlín, on fou nomenat professor extraordinari el 1934 Féu recerques importants en geometria superfícies cúbiques i de quart ordre i geometria projectiva, amb els seus mètodes sintètics Publicà Systematische Entwicklung der Abhängigkeit geometrischer Gestalten von Einander ‘Desenvolupament sistemàtic de la interdependència de les figures geomètriques’, 1932 i pòstumament 1882 aparegueren les seves obres completes Ideà, entre altres, el teorema que du el seu nom
fractal
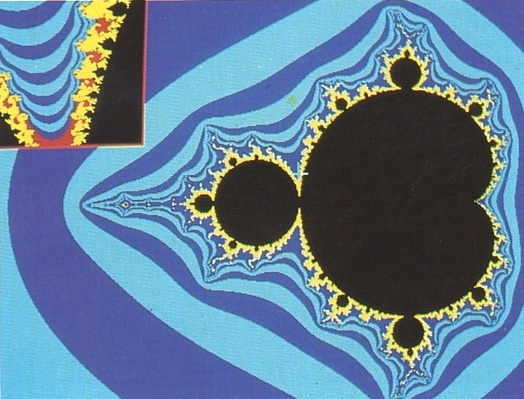
fractal Conjunt de Mandelbrot i un detall (corresponent al punt marcat per una creu blanca) [imatge obtinguda per ordinador al Departament d’Informàtica de la Universitat Autònoma de Barcelona]
Matemàtiques
Model matemàtic o objecte real que manté la seva forma essencial, fragmentada i irregular, tot i variant l’escala d’observació.
Les primeres fractals corbes de Von Koch, Peano, Sierpiński, etc aparegueren entre el 1875 i el 1925 com a contraexemples als intents de formalització de l’actual matemàtica Benoît Mandelbrot, els anys setanta, descobrí que aquests models serveixen per a representar la realitat Basant-se en els conceptes d’homotècia interna i de dimensió en el sentit de Hausdorff-Besikovič 1919, Mandelbrot definí les bases de la geometria fractal, que permet de modelitzar fenòmens com les turbulències, el cabal dels rius, el soroll blanc, la distribució de les galàxies, les estructures…
Pere Menal i Brufal
Matemàtiques
Matemàtic.
Llicenciat en matemàtiques per la Universitat de Barcelona l’any 1973, s’incorporà immediatament com a professor al Departament de Matemàtiques de la Universitat Autònoma de Barcelona, on ocupà el càrrec de Catedràtic d’àlgebra des del 1983 El 1987 obtingué el grau de doctor en matemàtiques amb la tesi Sobre radicals finits i linealitat residual de grups nilpotents Treballà en grups lineals, anells de grup, anells regulars de von Neumann i C *-àlgebres publicà més de trenta treballs de recerca en reconegudes revistes internacionals de matemàtiques, alguns d’ells en collaboració…
teoria dels jocs
Matemàtiques
Teoria que analitza matemàticament el comportament òptim dels diversos jugadors davant les possibles estratègies aplicables per a la resolució guanyadora del conflicte (joc).
L’abstracció de les formes comunes d’estratègia permet l’establiment d’uns models, anomenats jocs per comparació amb els jocs vulgars com els escacs o el bridge La teoria dels jocs d’estratègia, l’estudi dels quals fou iniciat per Émile Borel el 1921, fou establerta el 1928 per John von Neumann, el qual, juntament amb l’economista Oskar Morgenstern, publicà el 1944 la Theory of Games and Economic Behavior Bé que la majoria dels jocs actuals no poden ésser analitzats d’una manera matemàtica a causa de la immensa quantitat de dades que cal computar, molts poden ésser estudiats establint un…
reticle
Matemàtiques
Conjunt ordenat en el qual dos elements qualssevol tenen un suprem (la més petita de les fites superiors o elements majorants) i un ínfim (la més gran de les fites inferiors o elements minorants).
És anomenat també conjunt reticular Si C, ≤ és un “ordenat” que és reticle, donats a i b de C, existeix un element, anomenat suprem c = a ∪ b tal, que a ≤ c , b ≤ c , i si a < d i b < d és c < d i un element, dit ínfim , c = a ∩ b tal, que c < a, c < b i si d ≤a, d ≤ b , és d ≤ c El conjunt de parts d’un conjunt respecte a l’ordre definit per la inclusió és un reticle Exemple si A i B són dos conjunts qualssevol, el conjunt més petit que els conté és la seva reunió o suprem i el més gran contingut és la seva intersecció o ínfim La teoria de reticles nasqué amb l’estudi del…