Resultats de la cerca
Es mostren 130 resultats
espai normal
Matemàtiques
Espai topològic en el qual, donats dos espais tancats disjunts, n’hi ha dos d’oberts també disjunts que els contenen.
Un teorema d’Urysohn afirma que en un espai normal, donats dos espais tancats disjunts, hi ha una funció real contínua que pren el valor zero en l’un i el valor u en l’altre
bisector
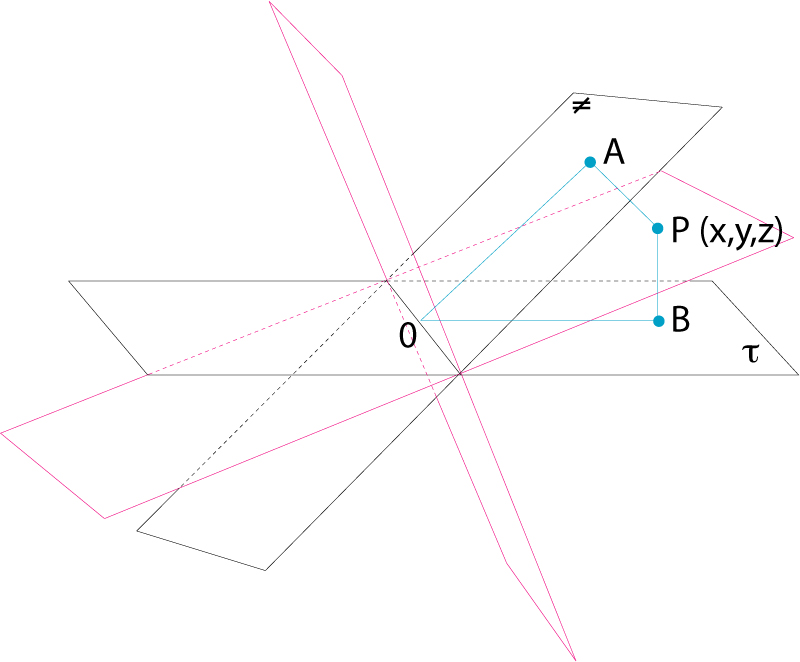
Plans bisectors dels quatre díedres formats per dos plans donats que es tallen
© Fototeca.cat
Matemàtiques
Lloc geomètric dels punts que equidisten dels dos plans costats d’un angle díedre, el qual, per tant, és dividit en dos díedres iguals.
Dos plans no parallels determinen quatre angles díedres, per als quals hom distingeix dos plans bisectors Per a cada díedre, un dels plans bisectors serà interior, i l’altre, exterior Si les equacions cartesianes de dos plans són A 1 x + B 1 y + C 1 z + D 1 = 0 i A 2 x + B 2 y + C 2 z + D 2 = 0, en una referència cartesiana normal, l’equació dels dos plans bisectors dels díedres que aquells determinen és
interpolació
Matemàtiques
Procediment que, donats els n valors y 1, y 2, ..., yi, ..., yn d’una funció y = g(x) en els punts x 1, x 2..., xi, ..., xn, permet de calcular, aproximadament, els valors de g(x) en punts intermedis als donats.
Més exactament, la interpolació consisteix a trobar una altra funció y = f x , d’un tipus escollit, que passi pels punts x i , y i Una primera aproximació és constituïda per la interpolació lineal , que consisteix a imposar que, entre cada dos punts consecutius dels donats, f x sigui un segment de recta En la interpolació de Lagrange , f x és un polinomi de grau n- 1 donat per la fórmula Si els punts x i constitueixen una progressió aritmètica, és emprada la interpolació de Newton càlcul de diferències diferència
resultant
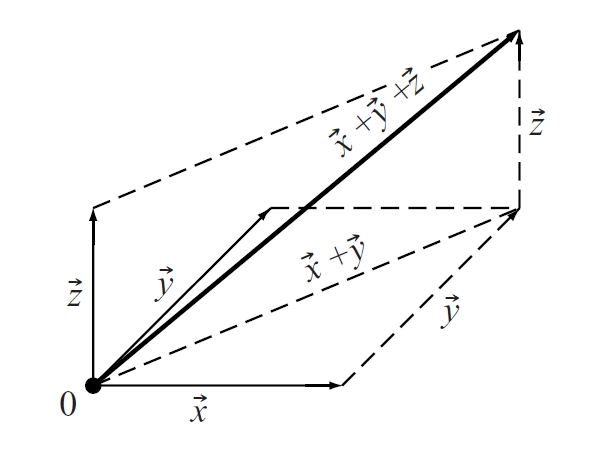
Resultant d’una suma de vectors
Física
Vector equivalent a la suma de dos vectors.
Donats dos vectors, hom n'obté la resultant per la regla del parallelogram cal construir un parallelogram que tingui per costats els vectors donats, i la resultant és aleshores la diagonal d’aquest parallelogram
plantilla
Electrònica i informàtica
Cadascuna de les fórmules d’interpolació utilitzades en el disseny amb ajuda d'ordinador que permeten de variar la forma d’una corba (dues dimensions) o d’una superfície (tres dimensions) si hom varia la posició dels punts pels quals aquestes passen o s’aproximen.
La més corrent és la plantilla cúbica hom pot demostrar que de totes les corbes que passen per una sèrie de punts donats, l’obtinguda amb la plantilla cúbica és la més suau sota algunes condiciones hom també pot demostrar que la corba dissenyada adopta la forma que tindria una vareta flexible que hom obligués a passar pels punts donats
capitular
Història
Precepte legal procedent dels sobirans carolingis i de llurs assemblees legislatives.
Tenia vigor per a tot l’imperi Alguns d’ells, però, tenien caràcter addicional als codis vigents en les regions annexades, com és el cas dels donats per Carlemany i Lluís el Piadós a favor dels hispans de les marques meridionals de l’imperi També en foren donats d’especials per els enviats missi , amb l’encàrrec d’inspeccionar regions concretes i de fer-hi complir les lleis generals Els capitulars carolingis tingueren vigència als comtats catalans del segle IX
polinomis de Laguerre
Matemàtiques
Polinomis en ℝ donats per l’expressió genèrica
Satisfan la fórmula de recurrència n +1 L n ₊₁ x + x-2n-1 L n x + n L n ₋₁ x = 0, i són solucions de l' equació diferencial de Laguerre, xy n + 1- x y’ + ny = 0 Els primers polinomis són L₀ x = 1, L₁ x = 1- x, L₂ x = 1-2 x + x 2 /2 Satisfan la següent ortogonalitat on és el símbol de Kronecker
polinomis d’Hermite
Matemàtiques
Polinomis en ℝ donats per l’expressió genèrica
Satisfan la fórmula de recurrència H n + 1 x - 2 xH n x + 2 nH n - 1 x = 0, i són solucions de l' equació diferencial d’Hermite, y n - 2 xy + 2 ny = 0 Els primers polinomis són H 0 x = 1, H 1 x = 2 x , H 2 x = 4 x 2 -2, etc Satisfan la següent ortogonalitat on δ p q és el símbol de Kronecker
polinomis de Legendre
Matemàtiques
Polinomis en ℝ donats per l’expressió genèrica
.
Satisfan la fórmula de recurrència n +1 P n + 1 x - 2n+1 P n x + nP n - 1 x =0, i són solucions de l' equació diferencial de Legendre , 1- x 2 y´´ - 2 xy ´ + n n +1 y = 0 Els primers polinomis són P 0 x = 1, P 1 x = x , P 2 x = 3 x 2 -1 /2 Satisfan la següent ortogonalitat on és el símbol de Kronecker
distància euclidiana
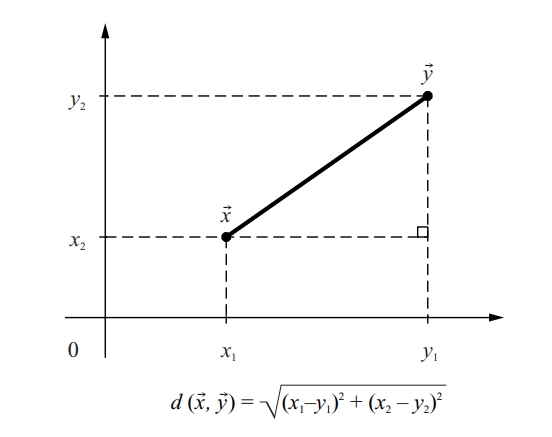
distància euclidiana
Matemàtiques
Distància definida a ℝ n.
Donats dos punts x = x 1 , , x n i y = y 1 , , y n de ℝ n , aquesta distància és definida per
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina